Ternarno pretraživanje

Autor: Maja Milas

O algoritmu

Kao što smo vidjeli u prethodnom članku, binarno pretraživanje pri svakom koraku dijeli niz koji pretražujemo na dva podniza te pomoću uvjeta određuje u kojem podnizu nastavljamo pretragu. Što se dogodi ako podniz podijelimo na tri dijela?

Algoritam ternarnog pretraživanja gotovo se potpuno podudara s binarnim te i njega koristimo za pronalazak broja $x$ u sortiranom nizu brojeva. Umjesto jedne srednje vrijednosti $mid$ ovoga puta biramo dvije i to na sljedeći način:

mid1 = l + (r-l)/3
mid2 = r – (r-l)/3

gdje su $r$ i $l$ desna i lijeva granica trenutnog podniza.

Sada uspoređujemo $x$ s vrijednostima $array[mid1]$ i $array[mid2]$. Ako je $x$ različit od obje vrijednosti (nismo pronašli rješenje), imamo tri slučaja:

1. $x$ je manji od $array[mid1]$ : $x$ se (ako ga ima) nalazi u intervalu $[l,mid1\rangle$
2. $x$ je veći od $array[mid2]$ : $x$ se (ako ga ima) nalazi u intervalu $\langle mid2,r]$
3. inače: $x$ se nalazi u intervalu $\langle mid1,mid2 \rangle$

Varijable $r$ i $l$ mijenjamo ovisno o slučaju koji je nastupio i ponavljamo postupak dok ne pronađemo rješenje ili provjerimo cijeli niz. Povučemo li analogiju s binarnim pretraživanjem, problem se ovdje pri svakom koraku svodi na $1/3$ prethodnog problema pa je složenost algoritma $O(log_3(n))$.

Ovoga ćemo puta pokazati rekurzivnu implementaciju (slična se može napraviti i za binarnu pretragu). Rekurzija vraća poziciju u nizu na kojoj se nalazi traženi broj ili $-1$ u slučaju da tog broja nema u nizu:

int ternary_search(int l, int r, int x) {
    if (r >= l) {
        int mid1 = l + (r-l)/3;
        int mid2 = r - (r-l)/3;

        if (array[mid1] == x)
            return mid1;
        if (array[mid2] == x)
            return mid2;
        if (x < array[mid1])
            return ternary_search(l, mid1-1, x);
        else if (x > array[mid2])
            return ternary_search (mid2+1, r, x);
        else
            return ternary_search(mid1+1, mid2-1, x);
    }
    return -1;
}

Implementacija na realnom intervalu

Ponekad želimo raditi pretraživanje na intervalu realnih brojeva. Ako koristimo ranije navedenu implementaciju, mogu se dogoditi pogreške pri uspoređivanju brojeva zato što računala nemaju beskonačnu preciznost i uvijek zaokružuju vrijednosti na nekoj decimali. Iz tog razloga nećemo provjeravati 'jednakost' dvaju brojeva nego razlikuju li se oni do na neki mali faktor. Prethodni bi se primjer mogao modificirati na sljedeći način:

double epsilon = 1e-7;
...
double ternary_search(double l, double r, double fx) {
    if (r-l > epsilon) {
        double mid1 = l + (r-l)/3;
        double mid2 = r - (r-l)/3;

        if (abs(f(mid1) - fx) < epsilon)
            return mid1;
        ...
    }
}

Lokalni ekstremi

U prethodnom smo primjeru proveli ternarnu pretragu nad sortiranim nizom brojeva, ali treba imati da umu da je za takve slučajeve binarna pretraga najčešće sasvim dovoljna (u kontekstu brzine algoritma). Ipak, ternarna je pretraga našla svoju primjenu u pronalaženju lokalnih ekstrema funkcija!

Zamislimo neku funkciju koja ima samo jedan ekstrem i neka je to maksimum. Zadatak nas pita koja točka na $x$-osi odgovara traženom maksimumu. Primjer takve funkcije prikazan je na slici. Maksimum funkcije postiže se u točki $A$. Za sve $x$-eve koji se nalaze lijevo od točke $A$ možemo reći da se nalaze u rastućem dijelu funkcije, dok za sve koji se nalaze desno možemo reći da se nalaze u padajućem dijelu.

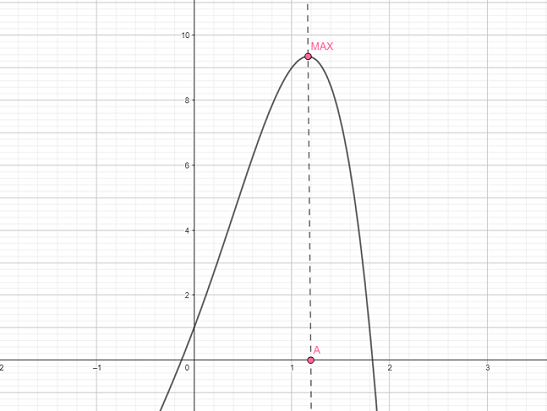
Kao i ranije, dijelimo interval na tri dijela uz pomoć $mid1$ i $mid2$ samo ovoga puta uspoređujemo vrijednosti funkcije u tim točkama. Mogućnosti su da se obje vrijednosti nalaze u rastućem dijelu, obje u padajućem dijelu ili po jedna u svakom od ta dva (prilikom razmišljanja o slučajevima razmislite o sve tri mogućnosti). Razlikujemo tri slučaja:

1. $f(mid1)<f(mid2)$ : Maksimum se ne može nalaziti lijevo od $mid1$ ($mid1$ se sigurno nalazi u rastućem dijelu), nastavljamo pretragu u intervalu $[mid1,r]$ .
2. $f(mid1)>f(mid2)$ : Maksimum se ne može nalaziti desno od $mid2$ ($mid2$ se sigurno nalazi u padajućem dijelu), nastavljamo pretragu u intervalu $[l,mid2]$ .
3. $f(mid1)=f(mid2)$ : Maksimum se nalazi negdje između $mid1$ i $mid2$ ($mid1$ je u rastućem dijelu, a $mid2$ u padajućem).

Više o ovoj temi pročitajte ovdje.

primijetite

Ovaj će algoritam raditi samo na funkcijama koje imaju isključivo jedan ekstrem. Takve funkcije nazivmo unimodalnima.

Što ako funkcija ima više od jednog ekstrema?

Traženje ekstrema funkcija ima veliku primjenu u znanosti i statističkoj obradi podataka, a često je bitan alat za numeričko rješavanje jednadžbi. Zamislite da ste izmjerili neke podatke i želite iz izračunate krivulje dobiti u kojoj se točno točki nalazi ekstrem funkcije. Rješenje problema zvuči malo glupavo, ali radi. Ideja je da okom pogledate graf funkcije i odaberete neki interval oko ekstrema koji vas zanima tako da ne obuhvatite niti jedan drugi lokalni ekstrem te funkcije. Potom provedete ternarnu pretragu isključivo na tom intervalu i dobili ste traženu točku (sveopća radost).