Segmentno stablo

Autor: Martin Josip Kocijan

Uvod

Često želimo postavljati upite nad intervalima nekog polja, npr. tražimo najveći element u nekom intervalu. Recimo da bismo naivnom implementacijom zadatka postigli vremensku složenost programa $O(QN)$, gdje je $Q$ broj upita a $N$ duljina polja. Tada za svaki upit imamo fiksnu složenost $O(N)$. Korištenjem tournamenta poboljšali bismo složenost svakog upita na $O(\log N)$ te ukupnu složenost na $O(Q \log N)$.

Tournament je modeliran kao potpuno binarno stablo. Općenito binarna stabla definiramo kao ukorijenjena stabla (povezan graf bez ciklusa) za koja vrijedi da svaki čvor ima najviše dvoje djece. Za potpuno binarno stablo dodatno vrijedi da su svi listovi (čvorovi bez djece) na istoj razini (udaljenosti od korijena).

Zaključujemo da svi čvorovi tournamenta osim listova imaju točno dvoje djece. Također, ako je $N$ visina stabla (najveća udaljenost od korijena), tournament ima točno $2^{N+1}-1$ čvorova.

Možemo na lijep način odabrati brojeve čvorova za lakše kretanje po stablu. Prvo korijen stabla označimo brojem $1$. Zatim za svaki čvor $X$ koji nije list označimo njegovo lijevo dijete s $2X$, a njegovo desno dijete s $2X+1$. Sada vrijedi da je roditelj čvora $X$ označen s $\left \lfloor{X/2}\right \rfloor$ (funkcija najveće cijelo). Važno je uočiti da su listovi označeni uzastopnim brojevima od $N$ do $2N-1$ ako se tournament sastoji od ukupno $2N-1$ čvorova.

U listove tournamenta spremamo originalni niz nad kojim vršimo upite. Zato veličinu tournamenta biramo tako da je broj listova veći ili jednak duljini niza u zadatku. Ako se oni ne podudaraju, dodajemo neutralne listove tako da oni ne utječu na rezultat. Svaki čvor tournamenta pokriva uniju intervala koje pokrivaju njegova djeca. Naposljetku korijen tournamenta pokriva čitav početni niz.

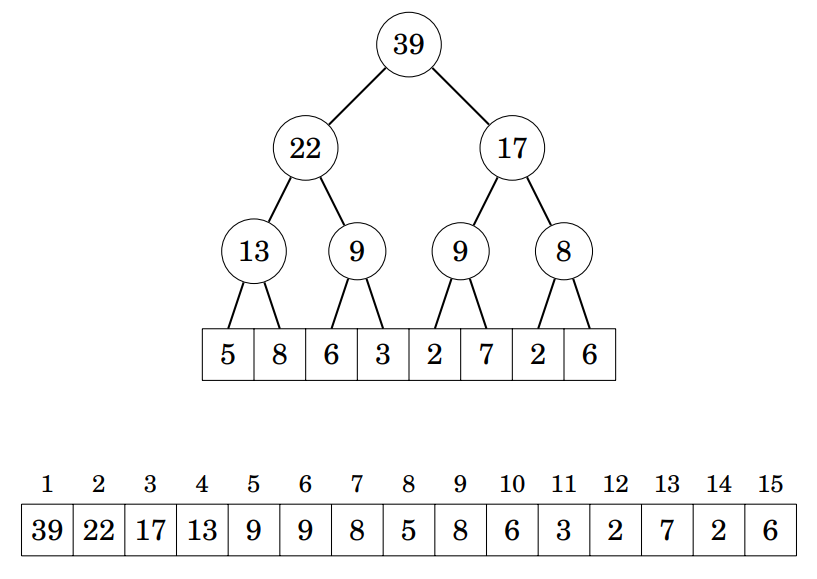
Na slici je prikazan primjer tournamenta nad poljem $[5, 8, 6, 3, 2, 7, 2, 6]$ od $8$ elemenata. Tournament sadržava ukupno $2 \cdot 8-1=15$ čvorova, te je njegova visina 3. U svakom je čvoru zapisana suma njegove djece. Pogledajmo na primjer čvor u kojem piše 22. Njega smo označili indeksom 2, dok njegova djeca imaju indekse $2 \cdot 2 = 4$, te $2 \cdot 2 + 1 = 5$, a roditelj mu ima indeks $\left \lfloor{2/2}\right \rfloor = 1$. Taj čvor u kojem piše 22 predstavlja interval $[1,4]$ u zadanom nizu, odnosno sumu od $[5, 8, 6, 3]$.

$\Large{\overbrace{\overbrace{\overbrace{5, 8}^{13}, \overbrace{6, 3}^{9}}^{22}, \overbrace{\overbrace{2, 7}^{9}, \overbrace{2, 6}^{8}}^{17}}^{39}}$

Ovdje je označen prekriven interval za svaki čvor u tournamentu. Na primjer, ako nas zanima suma elemenata u podintervalu $[2, 6]$, moramo zbrojiti parcijalne sume zapisane u tournamentu. U ovom slučaju to će biti one pod indeksima $9$, $5$ i $6$, jer su tamo zapisane sume podintervala $[2,2]$, $[3,4]$, te $[5,6]$. One su disjunktne a njihova je unija upravo naš traženi interval $[2, 6]$.

Implementacija

Koristimo tournament na ovakvom tipu zadatka:

Zadan je niz $A_i$ od $N$ elemenata, te $Q$ upita oblika:

• 1 X Y, želimo elementu $A_X$ dodati $Y$, ili
• 2 X Y, zanima nas suma elemenata $A_X + A_{X+1} + \ldots + A_{Y-1} + A_Y$

Treba paziti može li se desiti $X \gt Y$, i po potrebi zamijeniti tih dvaju brojeva, osim ako nije u zadatku zadano da ne može doći do toga.

Konstrukcija

Najosnovniji tournament sastoji se od jednog niza. Možemo ga spremiti kao globalnu varijablu, a ako trebamo više nizova možemo razmišljati o korištenju klase. Tada je jedan način da imamo klasu za čvor u kojoj pamtimo nekoliko vrijednosti vezanih uz taj čvor, pa imamo globalni niz s elementima tipa te klase. Drugi je način da u jednoj klasi imamo čitave nizove koji predstavljaju vrijednosti u tournamentima.

Možemo pomoću $N$ izračunati veličinu polja koje trebamo za tournament ako želimo uštedjeti na memoriji. Neka je $N'$ najmanja potencija broja $2$ koja nije manja od $N$. Tada će tournament imati $2N'-1$ čvorova od kojih će njih $N'$ biti listovi. Ovaj $N'$ moramo pamtiti jer će nam trebati kod kretanja kroz stablo. Evo primjer koda kako ga možemo dobiti:

int n2;
for (n2 = 1; n2 < n; n2 *= 2);

Najčešće ne moramo amortizirati složenost, a i svakako želimo kao duljinu globalnog polja staviti maksimalnu moguću duljinu koja se može pojaviti. Zato želimo uvijek imati neku konstantnu ogromnu veličinu tournamenta, pa tako možemo pročitati uvjet zadatka ($N \le 100\,000$) i dobiti da je $N' = 2^{17} = 131\,072$ dovoljan. Sad rezerviramo globalno polje za tournament od $2N'$ elemenata (ono je $1$-indeksirano!)

const int MAXN = 1e5;
const int OFFSET = 1 << 17; // 2^17

int n;
int a[MAXN]; // ulazni niz
int t[OFFSET * 2]; // tournament

Početnu inicijalizaciju tournamenta možemo napraviti u $O(N)$ pomoću jedne for petlje ili u $O(N \log N)$ tako da za svaki element niza zovemo funkciju za upit da promijenimo taj element niza. Ovaj način s for petljom izgleda ovako:

for (int i = 0; i < n; ++i) 
    t[OFFSET + i] = a[i];
for (int i = OFFSET - 1; i; --i)
    t[i] = t[i * 2] + t[i * 2 + 1];

Moramo osigurati da t[OFFSET + n], t[OFFSET + n + 1], itd. budu neutralni elementi pri operaciji zbrajanja, znači nula.

Upiti za ažuriranje (update)

Postoje dvije vrste upita, oni koji mijenjaju podatke koji su zapisani u tournamentu, te oni koji povlače informacije iz njega. Prvo ćemo napisati funkciju koja mijenja vrijednost nekog elementa u nizu.

Listovi tournamenta pokrivaju interval duljine $1$, odnosno samo jednog elementa niza. Zato ćemo upravo njih prve ažurirati prilikom promjene jednog elementa u nizu. Nakon toga moramo ažurirati vrijednost roditelja tog lista, pa roditelja od roditelja, itd.

// dodaje broj v elementu na poziciji pos
void update(int pos, int v) {
    pos += OFFSET;
    t[pos] = t[pos] + v;
    for (pos /= 2; pos; pos /= 2)
        t[pos] = t[pos * 2] + t[pos * 2 + 1];
    }
}

Upiti za očitanje (query)

Upiti nad intervalima nešto su složeniji. Naivnom implementacijom prošli bismo po cijelom intervalu i to je složenost $O(N)$ gdje je $N$ duljina niza. Da bismo dobili tournamentsku složenost $O(\log N)$ po intervalu, moramo interval razbiti na $O(\log N)$ disjunktnih podintervala. Svaki interval duljine $X$ možemo pokriti sa $X$ listova, ali taj se broj smanjuje kad spajamo čvorove sa zajedničkim roditeljem. Naime, na svakoj razini možemo imati maksimalno dva susjedna čvora, jer bi inače neki od njih imali zajedničkog roditelja. Pošto imamo $O(\log N)$ razina, imat ćemo $O(\log N)$ čvorova koje moramo pročitati.

Svaki čvor ima interval koji on obuhvaća. Možemo koristiti dva načina za bilježenje intervala, a nijedan nije bolji već je samo stvar navike. Jedan je način da kažemo da trenutni čvor pokriva interval $\left[ lo, hi \right)$ odnosno $[lo, hi-1]$, te je to ovaj prvi kod ispod. Drugi način jest da kažemo da čvor pokriva interval $[lo, hi]$, i to je drugi kod ispod. Interval $[X, Y]$ onaj je iz zadatka koji nas zanima, a njega označavaju varijable l i r. Opet moramo paziti na to je li interval otvoren ili zatvoren s desne strane.

int query(int cvor, int lo, int hi, int l, int r) {
    if (lo >= r || hi <= l) return 0;
    if (lo >= l && hi <= r) return t[cvor];
    int mid = (lo + hi) / 2;
    return  query(cvor * 2,     lo, mid, l, r) +
            query(cvor * 2 + 1, mid, hi, l, r);
}
// zanima nas A[X] + A[X+1] + ... + A[Y]
// pa cemo zvati query(1, 0, OFFSET, X, Y + 1)

int query2(int cvor, int lo, int hi, int l, int r) {
    if (lo > r || hi < l) return 0;
    if (lo >= l && hi <= r) return t[cvor];
    int mid = (lo + hi) / 2;
    return  query(cvor * 2,     lo, mid, l, r) +
            query(cvor * 2 + 1, mid + 1, hi, l, r);
}
// zanima nas A[X] + A[X+1] + ... + A[Y]
// pa cemo zvati query2(1, 0, OFFSET - 1, X, Y)

Pozivanje upita

Evo da vidimo na primjeru kako u glavnoj funkciji može izgledati pozivanje funkcija za upite.

for (int i = 0; i < q; ++i) {
    int qt, x, y;
    cin >> qt >> x >> y;
    --x;
    --y;
    if (qt == 1)
        update(x, y);
    else
        cout << query(1, 0, OFFSET, x, y + 1) << '\n';
    //  cout << query2(1, 0, OFFSET - 1, x, y) << '\n';
}

Pazimo da indekse elemenata u nizu indeksiramo počevši od $0$, dok su čvorovi indeksirani od $1$. Postoji OFFSET-1 čvorova manjih od OFFSET, a čvorovi koji odgovaraju elementima niza (jediničnim intervalima) numerirani su od OFFSET do OFFSET+n-1.

Primjeri

Dosad smo računali sumu intervala. Kao neutralni element koristili smo $0$, jer je $\operatorname{suma}(x,0)=x+0=x$. Ako bismo računali produkt intervala, kao neutralni element koristili bismo $1$, zbog $\operatorname{produkt}(x,1)=x \cdot 1=x$.

Često nas zanima koji je najmanji (ili najveći) element unutar nekog intervala. Tada kao neutralni element koristimo najmanji mogući broj ako tražimo maksimum, ili najveći mogući broj ako trebamo minimum. Za int to mogu biti -1e9 i 1e9. Kad računamo vrijednost roditelja pomoću djece, pišemo ovako nešto:

t[i] = min(t[i * 2], t[i * 2 + 1]);

Dolje je primjer kako može izgledati funkcija za upite nad intervalima.

int query(int cvor, int lo, int hi, int l, int r) {
    if (lo >= r || hi <= l) return 1e9;
    if (lo >= l && hi <= r) return a[cvor];
    int mid = (lo + hi) / 2;
    return  min(query(cvor * 2,     lo, mid, l, r),
                query(cvor * 2 + 1, mid, hi, l, r);
}
// zanima nas min({A[X], A[X+1], ..., A[Y]})
// pa cemo zvati query(1, 0, OFFSET, X, Y + 1)

Osim zbrajanja i množenja, mogu se pojaviti i druge asocijativne operacije kao što su bitovne operacije ili najveći zajednički djelitelj.

Tournament implicitno podržava razna binarna pretraživanja. Ako imamo izgrađen tournament za operaciju zbrajanja nenegativnih brojeva, možemo se kroz njega kretati da saznamo koji je najlijeviji element niza takav da je prefiks suma niza od početka niza do tog elementa veća ili jednaka $X$.

// trazi indeks i prvog elementa takvog da je a[0]+a[1]+...+a[i] >= X
int cvor = 1, lo = 0, hi = OFFFSET - 1;
int prefiks = 0;
while (lo < hi) {
    int mid = (lo + hi) / 2;
    if (prefiks + t[cvor * 2] >= X) {
        cvor = cvor * 2;
        hi = mid;
    } else {
        prefiks += t[cvor * 2];
        cvor = cvor * 2 + 1;
        lo = mid + 1;
    }
}
cout << lo << '\n';

Ako pak imamo tournament za traženje najmanjeg elementa nad nekim intervalom, možemo saznati neke druge stvari. Tako kretanjem kroz tournament možemo otkriti najdesniji element niza koji je manji od $X$.

// trazi najveci indeks i za koji vrijedi a[i] < X
int cvor = 1, lo = 0, hi = OFFFSET - 1;
while (lo < hi) {
    int mid = (lo + hi) / 2;
    if (t[cvor * 2 + 1] < X) {
        cvor = cvor * 2 + 1;
        lo = mid + 1;
    } else {
        cvor = cvor * 2;
        hi = mid;
    }
}
cout << lo << '\n';

Ovi kodovi rade ako postoji barem jedan zadovoljavajući indeks. Ako ne znamo postoji li on, moramo sami na kraju provjeriti zadovoljava li lo uvjete.

Lazy propagation

Nekad imamo operaciju za ažuriranje (update) nad svim brojevima u nekom intervalu. Jedan od načina za riješiti takav zadatak jest korištenje tournamenta s propagacijom. To se radi tako da se koristi dodatno polje koje predstavlja stablo propagacije u svim čvorovima. Treba se i drugačije napisati funkcija update, jako slično funkciji query. Još je ostala nova funkcija propagiraj(cvor) koja se poziva svaki put na početku izvođenja query i update.

Ideja je tournamenta s propagacijom da možemo svaki update nad intervalom rastaviti na $O(\log N)$ disjunktnih intervala predstavljenih čvorovima, isto kao query. Umjesto da mijenjamo svaki relevantan čvor, mi zapisujemo promjene u polje za propagaciju na indekse tih $O(\log N)$ čvorova. Svaki put kad želimo obraditi neki čvor, bilo u update ili u query, prvo želimo u njega upisati njegovu realnu vrijednost. Nakon toga propagiramo promjene u njegovu djecu i resetiramo propagaciju u trenutnom čvoru. Tako osiguravamo da će svaka promjena stići dokle god treba, pa čak i do listova. Također vrijedi da će se svaka propagacija odraziti nad predcima tog polja, zato propagiramo te čvorove u koje zapisujemo propagacije. Listovi nemaju djecu pa njih samo ažuriramo, a ne propagiramo ih dalje.

U nekim je slučajevima potrebno kombinirati propagacije, npr. ako se isti čvor ažurira više puta. Ako imamo operaciju koja dodaje $X$ svim elementima u nekom intervalu, dvije takve operacije koje dodaju $X_1$ i $X_2$ u propagaciju nekog čvora možemo kombinirati u jedinstvenu propagaciju iznosa $X_1+X_2$.

Jedan je tip operacije postavljanje svih elemenata intervala na neki broj $X$. Ako nas zanimaju najmanji brojevi u intervalima, čvor ažuriramo tako da ga promijenimo u $X$ (jer je svaki element kojeg on prekriva pretvoren u $X$). Ako nas zanimaju sume intervala, čvor ažuriramo tako da ga promijenimo u $X \cdot M$ gdje je $M$ veličina intervala koju čvor prekriva, npr. $hi-lo+1$.

Česti je i tip operacije za dodavanje broja $X$ svim elementima nekog intervala. Ako ovdje ispitujemo koji je najmanji broj u nekom intervalu, neki čvor ćemo ažurirati tako da mu dodajemo $X$ (jer je $\min(A+X,B+X)=\min(A,B)+X$). Ako pak tražimo sume nad intervalima, čvoru dodajemo $X \cdot M$ (varijabla $M$ je objašnjena iznad).

Primjer zadatka:

Zadan je niz $A_i$ od $N$ elemenata, te $Q$ upita oblika:

• 1 X Y Z, želimo elementima $A_X$, $A_{X+1}$, ..., $A_{Y-1}$, $A_Y$ dodati $Z$, ili
• 2 X Y, zanima nas suma elemenata $A_X + A_{X+1} + \ldots + A_{Y-1} + A_Y$

Rješenje:

#include <cstdio>
using namespace std;

const int MAXN = 1e5;
const int OFFSET = 1 << 17;

int n, q;
int a[MAXN];
int t[OFFSET * 2];
int p[OFFSET * 2];

void build()
{
    for (int i = 0; i < n; ++i) 
        t[OFFSET + i] = a[i];
    for (int i = OFFSET - 1; i; --i)
        t[i] = t[i * 2] + t[i * 2 + 1];
}

void propagiraj(int cvor, int lo, int hi)
{
    t[cvor] += (hi - lo) * p[cvor];
    if (cvor < OFFSET) {
        p[cvor * 2] += p[cvor];
        p[cvor * 2 + 1] += p[cvor];
    }
    p[cvor] = 0;
}

void update(int cvor, int lo, int hi, int l, int r, int x)
{
    propagiraj(cvor, lo, hi);
    if (lo >= r || hi <= l) return;
    if (lo >= l && hi <= r) {
        p[cvor] += x;
        propagiraj(cvor, lo, hi);
        return;
    }
    int mid = (lo + hi) / 2;
    update(cvor * 2,        lo, mid, l, r, x);
    update(cvor * 2 + 1,    mid, hi, l, r, x);
    t[cvor] = t[cvor * 2] + t[cvor * 2 + 1];
}

int query(int cvor, int lo, int hi, int l, int r) {
    propagiraj(cvor, lo, hi);
    if (lo >= r || hi <= l) return 0;
    if (lo >= l && hi <= r) return t[cvor];
    int mid = (lo + hi) / 2;
    return  query(cvor * 2,     lo, mid, l, r) +
            query(cvor * 2 + 1, mid, hi, l, r);
}

int main() {
    scanf("%d%d", &n, &q);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &a[i]);
    }
    build();
    for (int i = 0; i < q; ++i) {
        int qt, x, y, z;
        scanf("%d%d%d", &qt, &x, &y);
        --x;
        --y;
        if (qt == 1) {
            scanf("%d", &z);
            update(1, 0, OFFSET, x, y + 1, z);
        } else
            printf("%d\n", query(1, 0, OFFSET, x, y + 1));
    }
    return 0;
}
/*
10 5
1 2 3 4 5 6 7 8 9 10
2 2 9
1 4 10 1
2 3 7
1 3 6 2
2 1 5
*/