Uvod u grafove

Autor: Maja Milas

Što su grafovi?

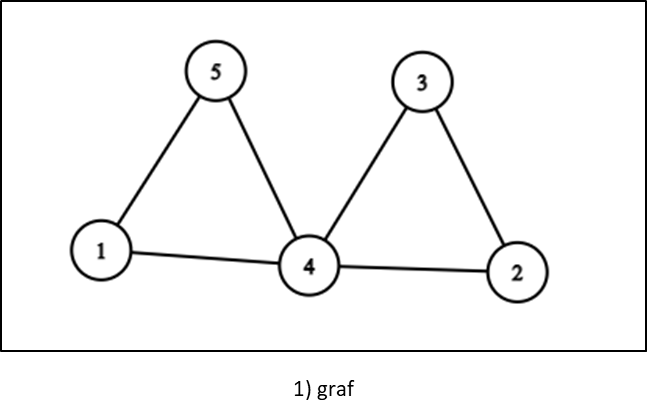
Graf je struktura podataka sastavljena od vrhova (čvorova, eng. node) i bridova (eng. edge). Vrhovi opisuju podatke, a bridovi veze između njih. Graf na slici 1 ima $5$ vrhova i $6$ bridova (i izgleda kao Toblerone).

Terminologija

Primijetit ćete da u ovom poglavlju ima užasno puno novih pojmova. Neke koristimo non-stop, a neki se gotovo nikad ne pojavljuju, ali svakako se nemojte opterećivati ako odmah sve na popamtite. Na početku se fokusirajte na dio 'Osnovni pojmovi', a ostalo će doći s vremenom.

Osnovni pojmovi

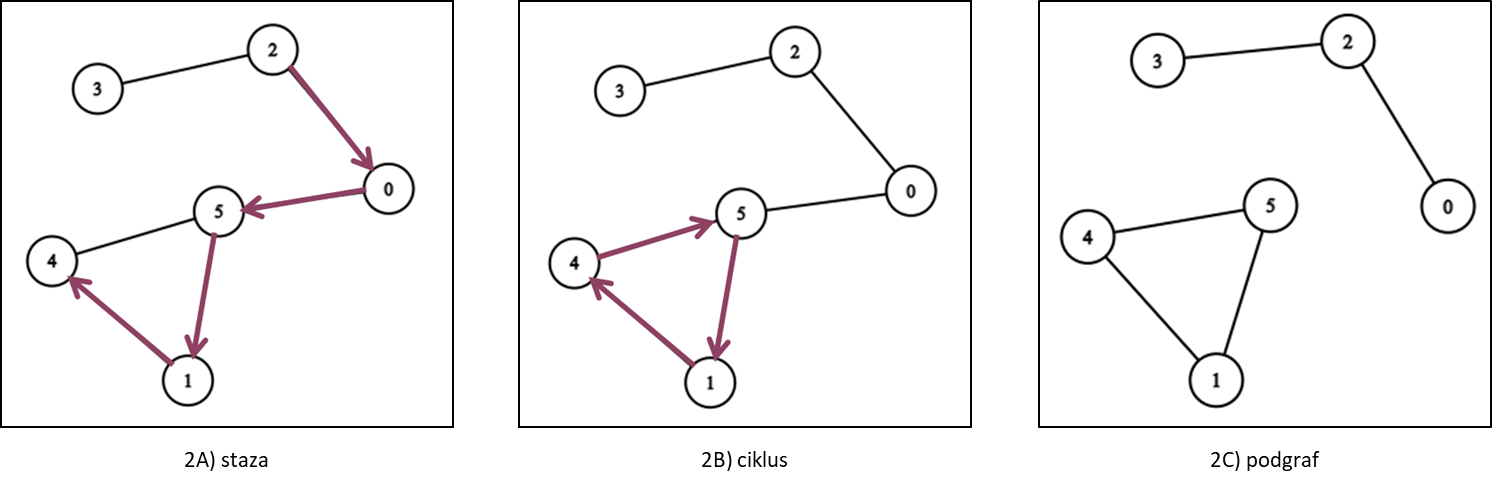
• staza (2A) = vodi od vrha a do vrha b (ne ponavljaju se bridovi)
  • put je staza u kojoj se ne ponavljaju vrhovi (osim ako je ciklus)
  • duljina staze je broj bridova u stazi ili suma težina bridova ako je u pitanju težinski graf
• ciklus (2B) = put koji počinje i završava na istom vrhu
• podgraf (2C) = (eng. subgraph) graf napravljen od podskupa vrhova i bridova nekog originalnog grafa

Povezanost grafa

Graf u kojem postoji put između svaka dva vrha je povezan. Na gornjim je slikama graf 2A povezan dok graf 2C nije povezan jer ne postoji put između 0 i 1. Povezani dijelovi grafa zovu se komponente. Graf 2C ima dvije komponente: 5 i 3.

Stablo

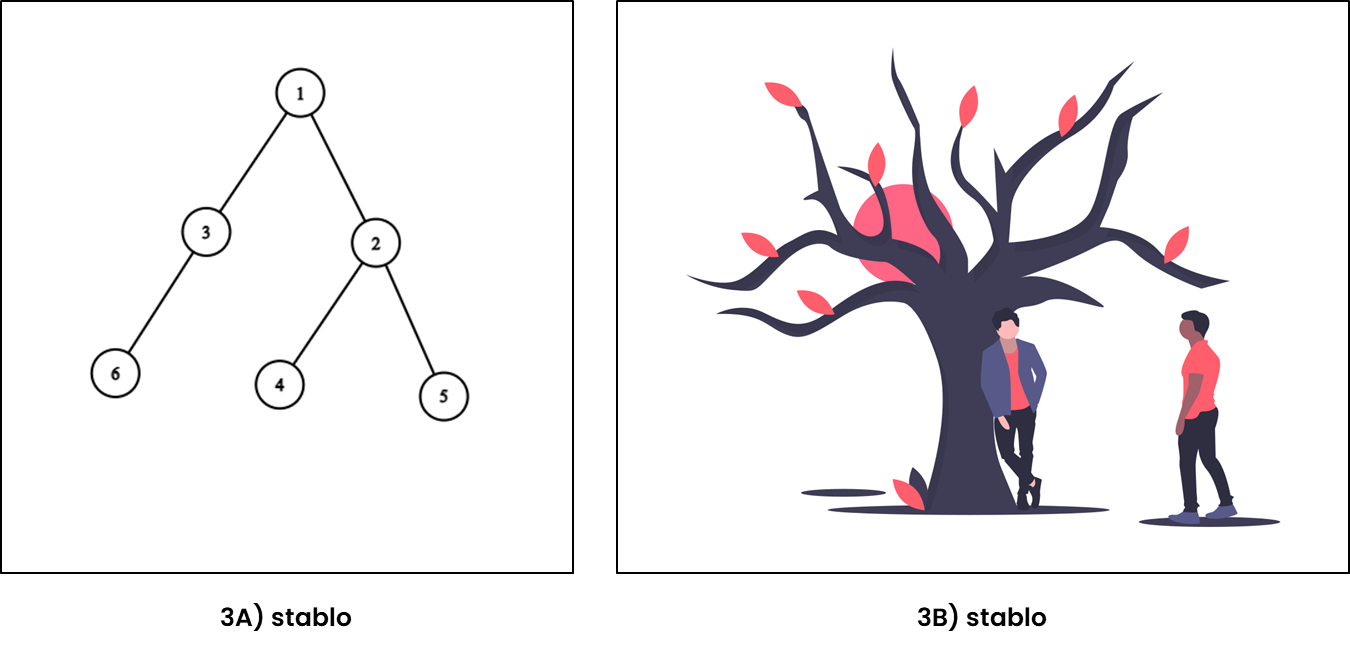
Stablo (3A) je povezan graf koji se sastoji od $n$ vrhova i $n-1$ bridova te nema cikluse. Postoji jedinstven put između bilo koja dva vrha stabla. Vrhovi koji imaju samo jednog susjeda zovu se listovi stabla (eng. leaf).

Kada prikazujemo stabla često biramo jedan vrh kojeg nazovemo korijenom (eng. root) od kojeg krećemo crtati stablo. Kažemo da su njegovi prvi susjedi njegova djeca, a on je njihov roditelj. Preostali susjedi njegove djece su njihova djeca i tako dalje.

Bridovi

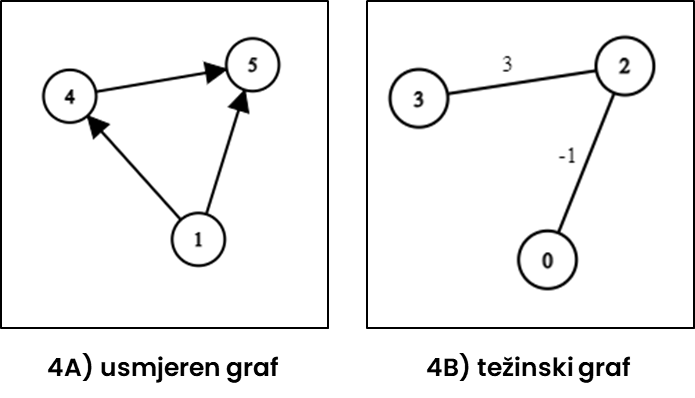
• usmjeren graf (4A) = (eng. directed graph) graf u kojem se preko brida može prijeći samo u jednom smjeru
• težinski graf (4B) = (eng. weighted graph) graf u kojem je svakom bridu pridružena težina; težina se najčešće interpretira kao duljina brida
  • duljina puta u težinskom grafu određuje se kao zbroj težina bridova koji čine put

Susjedi

Za dva vrha kažemo da su susjedni (eng. neighbours ili adjacent) ako između njih postoji brid. Stupanj (eng. degree) nekog vrha je broj njegovih susjeda. Na grafu 4B vrh 2 ima susjede 0 i 3 pa je njegov stupanj 2.

Graf je regularan (eng. regular) ako su svi vrhovi istog konstantnog stupnja $d$, a potpun (eng. complete) ako je stupanj svakog vrha $n-1$ (gdje je $n$ ukupan broj vrhova). U potpunom grafu postoji brid između svaka dva vrha.

Vrhovi usmjerenog grafa imaju ulazni i izlazni stupanj. Ulazni stupanj (eng. indegree) vrha je broj bridova koji završavaju u tom vrhu, a izlazni stupanj (eng. outdegree) je broj bridova koji počinju u tom vrhu.

Bojanje grafova

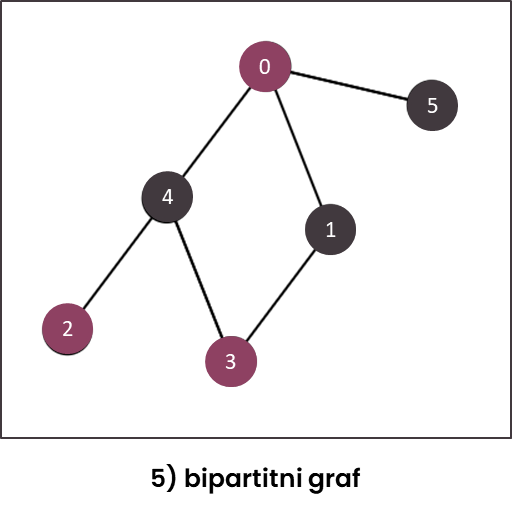
Pri bojanju grafa (eng. colouring) svakom je vrhu dodijeljena boja tako da ne postoje dva susjedna vrha iste boje. Graf je $k$-obojiv ako ga možemo obojiti koristeći $k$ boja, a specijalno ako je $k=2$ kažemo da je graf bipartitni (5) (eng. bipartite graph). Kromatski broj grafa je najmanji $k$ za koji je graf $k$-obojiv.

Zašto učiti grafove?

Puno se problema u programiranju može prikazati pomoću grafova. Tipičan primjer takvog problema je mreža cesta i gradova. Ceste prikazujemo kao bridove, a gradove kao vrhove. Sada se možemo pitati postoji li put između neka dva grada ili, ako znamo da postoji više puteva, kolika je duljina najkraćeg puta. Koji gradovi čine povezanu cjelinu unutar koje postoji put između svih gradova? Ulice unutar gradova možemo prikazati kao usmjereni težinski graf gdje je težina brida duljina ulice, a smjer određuje je li ulica dvosmjerna ili jednosmjerna.

Ipak, nisu svi problemi s grafovima tako očiti. Ponekad ćemo grafom prikazivati odnose zaposlenika u nekoj tvrtki ili obiteljsko stablo. Više-manje svi problemi koji se mogu riješiti dinamičkim programiranjem mogu se gledati kao problemi s grafovima.

U svakom slučaju, ne želite preskočiti grafove! 😄