Union-find struktura

Autor: Maja Milas

Zadatak

Zamislite da u nekoj zemlji postoji $n$ gradova i $m$ cesta koje ih povezuju, a u svakom gradu na početku živi $x$ ljudi. Tijekom vremena, neke ceste postaju nestabilne i urušavaju se. U tom svijetu provodite 2 oblika queryja:

• D K - urušila se cesta K
• P A x - populacija A-tog grada postala je x

Vi ste mladi nadobudni geograf i želite nakon svakog upita odgovoriti koji je broj stanovnika trenutno najnaseljenije regije. Regija je definirana kao podskup gradova u kojem se može doći cestom između bilo koja dva.

Ovaj je zadatak ovdje samo za ilustraciju, ali probajte malo razmisliti kako biste ga riješili. Puni tekst problema možete naći ovdje.

Struktura

Union find (nekad i disjoint set) je struktura podataka koja elemente raspodjeljuje u skupove. Za dva skupa kažemo da su disjunktni (disjoint) ako ne postoji element koji pripada u oba skupa. Struktura je napravljena tako da svaki skup ima svoga predstavnika (representative), a elementi skupa su preko lanca povezani s predstavnikom. Na slici ispod su prikazana tri skupa, {1, 4, 7}, {5} i {2, 3, 6, 8}. Predstavnici skupova su redom 4, 5 i 2.

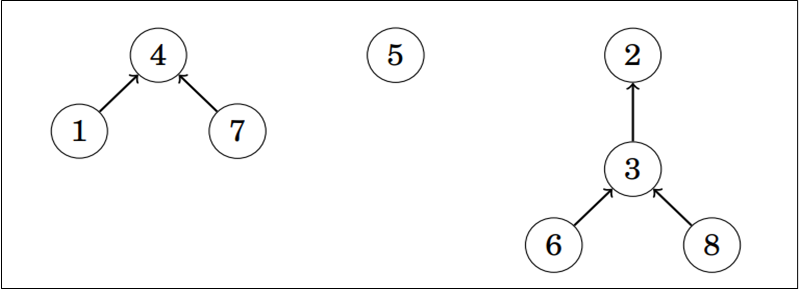
Predstavnike također možemo gledati na razini lanca. Npr. reći ćemo da elementi 6 i 8 imaju za predstavnika element 3.

Union find podržava dvije operacije:

• unite($a$,$b$) - operacija koja spaja skup koji sadrži element $a$ sa skupom koji sadrži element $b$
• find($x$) - operacija koja traži predstavnika skupa koji sadrži element $x$

bitno

Obje operacije rade u logaritamskoj složenosti.

Dva skupa možemo spojiti tako da povežemo njihove predstavnike. Na slici ispod spojili smo skupove {1, 4, 7} i {2, 3, 6, 8} tako da 2 postaje novi predstavnik, a skup koji u konačnici dobivamo je {1, 2, 3, 4, 6, 7, 8}.

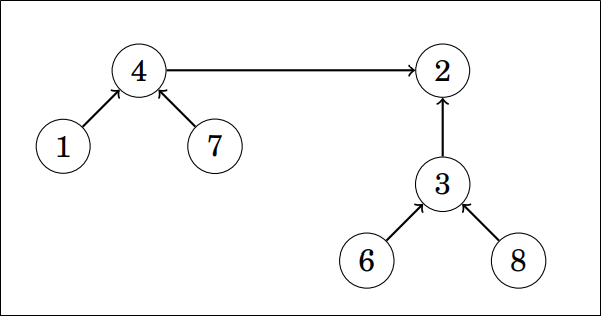
Pokazuje se da je prilikom spajanja uvijek efikasnije spajati manji skup na veći. Na taj je način naš skup više 'razgranat' i možemo postići logaritamsku složenost pretraživanja.

Implementacija

Za ovu ćemo implementaciju koristiti 1D polje link gdje će na i-tom mjestu pisati predstavnik i-tog elemenata te polje len gdje ćemo na mjestima na kojima su predstavnici pisati veličina skupa kojeg predstavljaju. Na gornjoj bi slici bilo link[7]=4 i len[2]=7.

Na početku svaki element pripada svom skupu pa je i sam svoj predstavnik. Duljina svih skupova je $1$.

for(int i=0; i<n; i++) link[i] = i;
for(int i=0; i<n; i++) len[i] = 1;

Funkcija find($x$) vraća predstavnika skupa koji sadrži element $x$. Pretraživanje obavljamo penjanjem po lancu dok ne dođemo do predstavnika.

int find(int x) {
    while(x != link[x]) x = link[x];
    return x;
}

Možemo napisati i funkciju same(a,b) koja provjerava jesu li dva elementa u istom skupu.

bool same(int a, int b) {
    return find(a) == find(b);
}

Funkcija unite($a$,$b$) spaja skupove koji sadrže element $a$ i element $b$. Prvo nalazimo njihove predstavnike i provjeravamo koji je skup manji, a potom spajamo manji skup na veći.

void unite(int a, int b) {
    a = find(a);
    b = find(b);
    if(len[a] < len[b]) swap(a,b);
    len[a] += len[b];
    link[b] = a;
}

Pokušajte sada sami napisati kod koji bi rješavao problem s početka lekcije. Happy coding!