Pretraživanje grafova

Autor: Ivan Vlahov

Većina algoritama nad grafovima koje ćete koristiti za natjecateljsko programiranje temelje se na nekakvom obilasku svih čvorova grafa kako bi se iz tog obilaska mogli izvući nekakvi zaključci. Upravo iz tog razloga bitno je razumijeti pretraživanje u dubinu - depth first search, i pretraživanje u širinu - breadth first search. Razumijevanjem tih metoda pretraživanja i njihovih karakteristika moći ćete ih koristiti za jako široku paletu problema i po potrebi ih adaptirati za specifične probleme.

Depth First Search

Pretraživanje u dubinu, depth first search, ili ukratko DFS, metoda je obilaska čvorova u kojoj prelazimo s jednog čvora na drugi dok god nalazimo nove, neposjećene čvorove. U slučaju da iz trenutnog čvora ne možemo obići neki novi čvor, vraćamo se na čvor iz kojeg smo došli, pokušavamo ići na neposjećene čvorove itd. Pretraživanje završava kad se posjete svi čvorovi do kojih postoji put iz prvog čvora nad kojim je DFS pozvan.

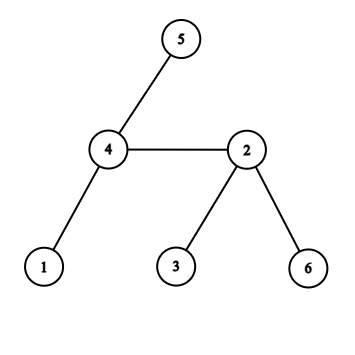
Uzmimo na primjer graf sa slike. Recimo da za sljedeći čvor u obilasku biramo prvo onaj neposjećeni čvor s najmanjim indeksom, te da je početni čvor onaj s indeksom 1. Označimo njega kao posjećenog, te iz njega prelazimo na neposjećeni susjedni čvor s najmanjim indeksom, u ovom slučaju čvor 4. Ponavljamo postupak za čvor 4: označavamo ga kao posjećenog, njegovi neposjećeni susjedi su 2 i 5 - prelazimo na čvor 2. Označimo čvor 2 kao posjećenog, prelazimo na čvor 3. Označimo čvor 3 kao posjećenog. Iz čvora 3 nemamo više gdje ići, pa se vraćamo u čvor iz kojeg smo došli, a to je čvor 2. Opet tražimo neposjećenog susjeda čvora 2 s najmanjim indeksom - sad je to čvor 6. Prelazimo na njega, označimo ga kao posjećenog i vraćamo se opet na 2 jer nemamo kamo drugdje iz 6. Sad ni 2 više nema neposjećenih susjeda, pa se vraćamo u 4. Iz 4 idemo u 5, iz 5 se vraćamo u 4, te iz 4 natrag u 1, gdje pretraživanje završava.

Kad bismo prilikom prvog ulaska u svaki čvor ispisali njegov indeks, dobili bismo sljedeći ispis:

1 4 2 3 6 5

DFS se može implementirati na više načina. Najčešći i jednostavan način implementacije je rekurzivnim pozivima - zadani čvor označimo kao posjećenog, a zatim redom pozivamo DFS na svim njegovim neposjećenim susjedima.

// mozete graf deklarirati globalno
// ili, ako ne zelite, proslijediti 
// referencu na graf funkciji dfs
// MAXN je neka konstanta, npr. najveci
// moguci broj cvorova iz teksta zadatka
vector<vector<int>> graph(MAXN);

// isto vrijedi i za polje posjecenih cvorova
// visited[i] je true ako je cvor i posjecen,
// inace false
// na pocetku je false za sve cvorove
vector<bool> visited(MAXN, false);

void dfs(int node) {
    visited[node] = true;

    // radi nesto s cvorom, npr. ispis indeksa
    cout << "Usao u cvor " << node << "\n";

    for(auto &it : graph[node]) {
        if(!visited[it]) dfs(it);
    }
}

Pozovemo li sad ovu funkciju na grafu sa slike:

graph[1] = {4};
graph[2] = {3, 4, 6};
graph[3] = {2};
graph[4] = {1, 2, 5};
graph[5] = {4};
graph[6] = {2};

dfs(1);

Dobit ćemo očekivani ispis:

Usao u cvor 1
Usao u cvor 4
Usao u cvor 2
Usao u cvor 3
Usao u cvor 6
Usao u cvor 5

primijetite

Ne postoji razlika u implementaciji ako se radi o usmjerenom grafu.

Bitna svojstva i varijacije DFS-a

Ako su nakon DFS-a svi čvorovi neusmjerenog grafa označeni kao posjećeni, graf je povezan. Također koristeći DFS možemo pronaći broj komponenti nepovezanog grafa tako što iteriramo kroz sve čvorove i pozivamo DFS za one koji dosad nisu posjećeni. Broj poziva DFS-a je ujedno i broj komponenti.

int components = 0;

for(int i=1; i<=n; i++) {
    if(!visited[i]) {
        components++;
        dfs(i);
    }
}

Također, ako prilikom DFS-a nijednom ne naiđemo na posjećen čvor (osim onoga iz kojeg smo došli u trenutni čvor), možemo zaključiti da je graf stablo jer u stablima vrijedi da između dva čvora postoji točno jedan put.

bool graphIsATree = true;

void checkIfGraphIsATree(int node, int pred) {
    visited[node] = true;

    for(auto &it : graph[node]) {
        if(it == pred) continue;

        if(visited[it]) {
            graphIsATree = false;
            return;
        }else{
            checkIfGraphIsATree(it, node);
        }
    }
}

Ako smo sigurni da je graf stablo (npr. iz teksta zadatka), polje visited nam ni ne treba:

// izvan maina

void dfsOnTree(int node, int pred) {
    // radi nesto s cvorom

    for(auto &it : graph[node]) {
        if(it == pred) continue;

        dfs(it, node);
    }
}

// u mainu

// ne mora nuzno prvi argument biti 1,
// moze biti koji god cvor hocete
dfsOnTree(1, -1);

Ako naiđemo na već posjećeni čvor, a koji nije onaj čvor iz kojeg smo došli u trenutni čvor, možemo zaključiti da su trenutni čvor i taj već posjećeni čvor dio istog ciklusa. Ako pri pozivu DFS-a zapamtimo na kojoj smo dubini rekurzije, možemo jako jednostavno izračunati duljinu ciklusa na koji smo naišli.

Pomoću jedne varijacije DFS-a možemo i obići sve moguće jednostavne putove u grafu - nakon što obradimo cvor i pozovemo DFS za njegove neposjećene susjede, vratimo taj čvor nazad u neposjećeno stanje i nastavimo obrađivati prošli čvor. Ako pozovemo takav DFS za sve čvorove u grafu, obići ćemo sve moguće jednostavne putove u grafu.

// mozemo ovo koristiti za pracenje trenutnog puta
vector<int> currentPath;

void tryAllPaths(int node) {
    visited[node] = true;
    currentPath.push_back(node);

    for(auto &it : graph[node]) {
        if(!visited[it]) {
            tryAllPaths(it);
        }
    }

    for(auto &it : currentPath) {
        cout << it << " ";
    }
    cout << "\n";

    currentPath.pop_back();
    visited[node] = false;
}

Pozovemo li ovu funkciju za primjer sa slike:

tryAllPaths(1);

Dobit ćemo sljedeći ispis:

1 4 2 3 
1 4 2 6 
1 4 2 
1 4 5 
1 4 
1

U ovom primjeru nalazimo samo jednostavne putove koji počinju u čvoru 1, a jednostavnom iteracijom po svim čvorovima možemo pronaći sve moguće jednostavne putove iz svih čvorova.

Breadth First Search

Drugi način pretraživanja grafova jest pretraživanje u širinu. Ideja ove metode je da čvorove obrađujemo po "slojevima" - obradimo početni čvor, taj čvor je dio sloja 0, zatim njegove neposjećene susjede - sloj 1, pa neposjećene susjede čvorova iz sloja 1 - oni su dio sloja 2, i tako dalje dok ne obradimo sve čvorove do kojih postoji put iz početnog čvora.

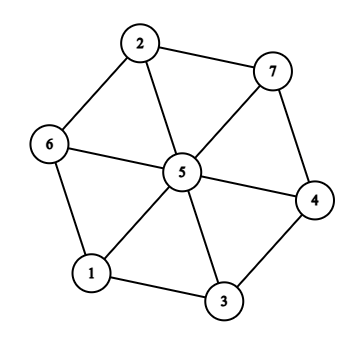
Započnemo li pretraživanje u širinu na grafu sa slike u čvoru 1, i ako opet pretpostavimo da su susjedi sortirani uzlazno po indeksu, algoritam će se ponašati na sljedeći način. Obradimo čvor jedan, označimo ga kao posjećenog, te redom posjećujemo njegove neposjećene susjede - to su redom čvorovi 3, 5 i 6. Nakon toga posjećujemo sve neposjećene susjede čvora 3 - to je čvor 4, pa neposjećene susjede čvora 5 - to su čvorovi 2 i 7, pa neposjećene susjede čvora 6 - takvih čvorova više nema. Nakon toga pokušavamo posjetiti neposjećene susjede čvorova 4, 2 i 7, međutim oni nemaju niti jednog neposjećenog susjeda, pa algoritam završava.

Kad bismo prilikom posjeta čvora ispisali njegov indeks, dobili bismo ovakav ispis:

1 3 5 6 4 2 7

Implementacija BFS-a temelji se na korištenju reda. Početni čvor dodamo u red te ponavljamo sljedeći postupak sve dok se red ne isprazni: skinemo čvor s početka reda, ako već nije posjećen obradimo ga, označimo ga kao posjećenog, te na kraj reda dodamo sve njegove neposjećene susjede.

U C++-u ta implementacija izgleda ovako, npr. za graf sa slike i početni čvor 1:

graph[1] = {3, 5, 6};
graph[2] = {5, 6, 7};
graph[3] = {1, 4, 5};
graph[4] = {3, 5, 7};
graph[5] = {1, 2, 3, 4, 6, 7};
graph[6] = {1, 2, 5};
graph[7] = {2, 4, 5};

queue<int> q;

// pocetni cvor rucno dodajemo u red
q.push(1);

while(!q.empty()) {
    int node = q.front();
    q.pop();

    if(visited[node]) continue;
    visited[node] = true;

    // radi nesto s cvorom, npr. ispis indeksa
    cout << "Usao u cvor " << node << "\n";

    for(auto &it : graph[node]) {
        if(!visited[it]) {
        q.push(it);
        }
    }
}

Ovaj isječak koda daje očekivani ispis:

Usao u cvor 1
Usao u cvor 3
Usao u cvor 5
Usao u cvor 6
Usao u cvor 4
Usao u cvor 2
Usao u cvor 7

primijetite

Za razliku od DFS-a, u BFS-u moramo raditi provjeru je li neki cvor posjećen i za taj sami cvor i za njegove susjede. Razlog je činjenica da dva različita čvora koja su dio istog sloja mogu dodati istog susjeda u red dva puta, pa se moramo pobrinuti da se čvor ne obradi opet drugi put kad se nađe na početku reda.

Bitna svojstva i varijacije BFS-a

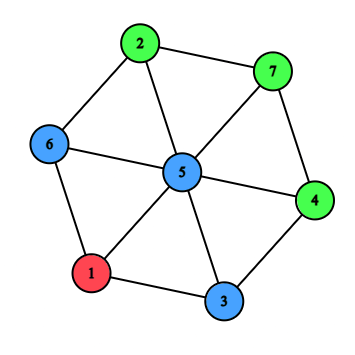
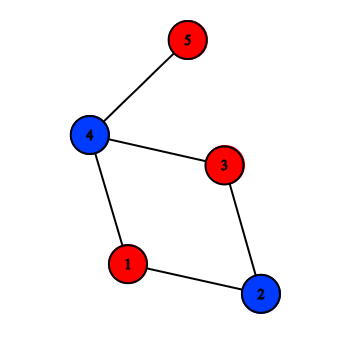
Jedno zanimljivo svojstvo BFS-a jest da pomoću njega možemo provjeriti je li graf bipartitan ili ne. Ideja jest da početni čvor obojimo u jednu boju (npr. crvenu), postavimo ga u red i ponavljamo sljedeće korake: skinemo čvor s početka reda, provjerimo jesu li njegovi susjedi obojani - ako postoji ijedan susjed koji je obojan u istu boju kao i trenutni čvor, graf nije bipartitan. U suprotnom, bojamo sve neobojane susjede u obrnutu boju od one trenutnog čvora (plavu ako je crven, crvenu ako je plav), dodajemo ih u red i nastavljamo dok se red ne isprazni.

Drugo zanimljivo, a često i jako korisno svojstvo BFS-a jest da se pomoću njega u netežinskim grafovima može pronaći duljina najkraćeg puta između nekog početnog čvora i svih ostalih čvorova grafa. Ideja je vrlo jednostavna - do čvorova u prvom sloju BFS-a sigurno ne postoji kraći put - oni su za 1 brid udaljeni od početnog čvora. Duljina najkraćeg puta do čvorova u drugom sloju je sigurno 2, jer su za 1 udaljeni od čvorova iz prvog sloja, a da je manja, već bismo ih obradili u prvom sloju. Slično vrijedi i za čvorove idućih slojeva.