Preskoči na glavni sadržaj

MST

Autor: Maja Milas

Minimalno razapinjuće stablo (MST)​

Razapinjuće stablo nekog grafa je podgraf koji se sastoji od svih njegovih vrhova i nekih bridova tako da postoji put između svaka dva vrha. Kao i obična stabla, razapinjuća stabla su povezana i nemaju cikluse. MST je razapinjuće stablo čiji je zbroj težina bridova minimalan.

mst1

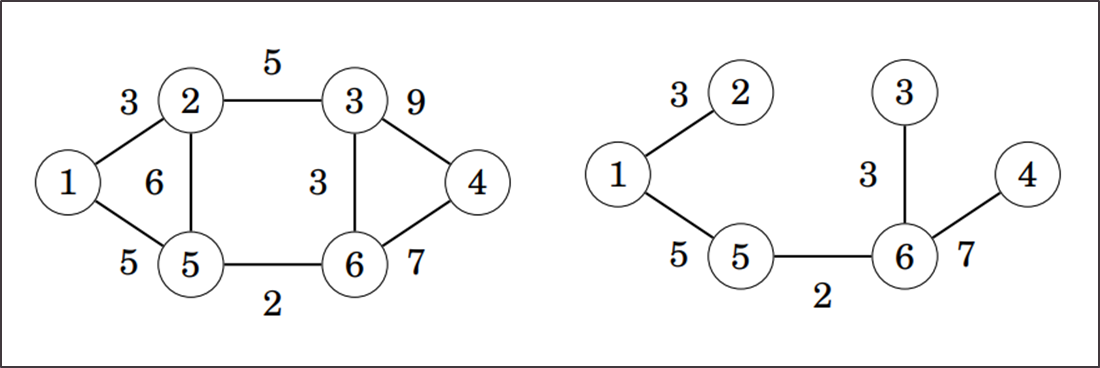
Na slici lijevo prikazan je neki graf, a desno njegov MST. Sličnom logikom možemo konstruirati i maksimalno razapinjuće stablo (ima maksimalnu sumu težina bridova).

primijetite

Minimalno (maksimalno) razapinjuće stablo ne mora biti jedinstven graf.

Kruskalov algoritam​

Kruskalov je algoritam jedan u nizu algoritama koji konstruiraju MST. Na početku ćemo u graf dodati samo vrhove, a potom ćemo dodavati bridove po redu od manjih prema većima. Algoritam dodaje brid u stablo ako dodavanjem tog brida ne nastaje ciklus. Kako bi to jednostavno provjeravali, koristit ćemo Union find strukturu.

Pogledajmo kako bi Kruskalov algoritam radio za graf s prethodne slike. Na početku u stablu imamo samo vrhove i svaki vrh čini zaseban skup. Bridove smo sortirali po težinama.

mst2

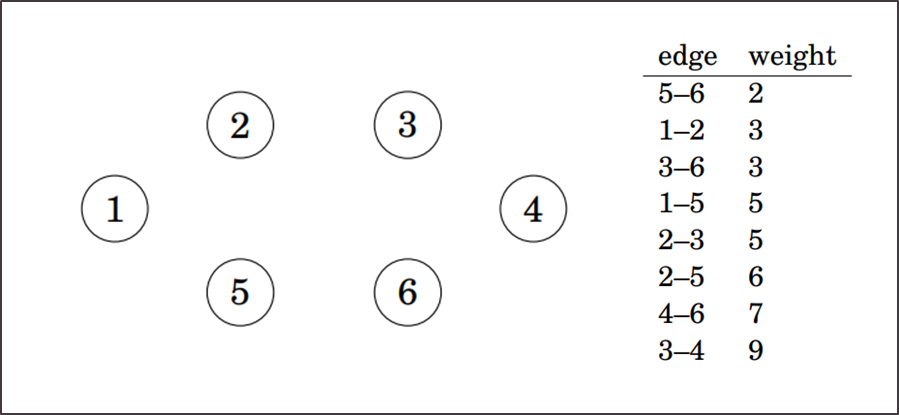
Prvo dodajemo brid 5-6 te skupove {5} i {6} spajamo funkcijom unite (lijevo). Nakon toga dodajemo bridove 1-2, 3-6 i 1-5 na sličan način spajamo odgovarajuće skupove (desno).

mst3

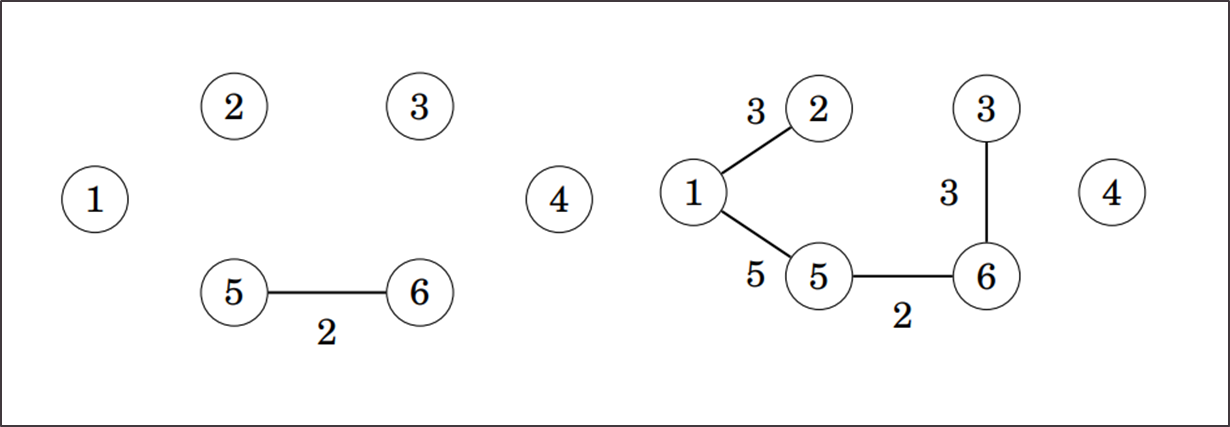
Sada u strukturi imamo 2 skupa: {1,2,3,5,6} i {4}. Sljedeći brid na popisu je 2-3, ali njega nećemo dodavati jer su 2 i 3 unutar iste komponente (dodavanjem bi nastao ciklus). Slično je i za brid 4-5. Na kraju dodamo brid 4-6 i gotovi smo (jej!).

mst4
primijetite

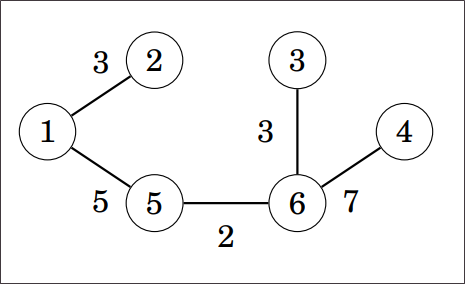
Kruskalov algoritam spada u pohlepne algoritme.

Zašto ovo radi?​

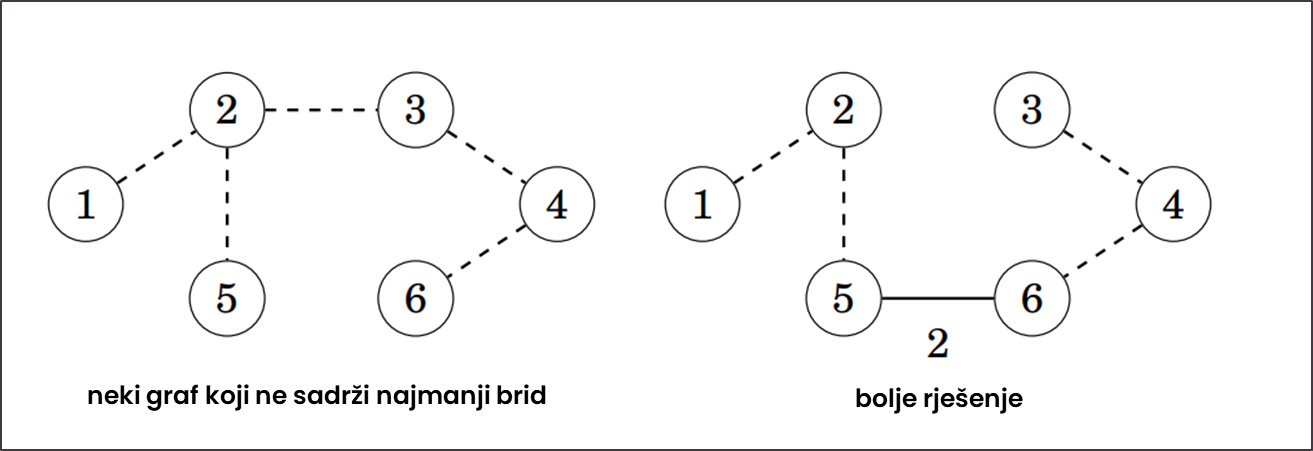
Ovaj će algoritam uvijek u MST dodati najmanji brid, ali zamislimo da postoji situacija kada to nije rješenje. U našem bi primjeru to značilo da postoji bolje razapinjuće stablo koje ne sadržava brid 5-6. Međutim, ovo ne može biti rješenje zato što uvijek možemo maknuti jedan brid iz takvog grafa i zamijeniti ga s bridom 5-6 što sigurno smanjuje rješenje (primjer na slici ispod). Sličnim razmišljanjem možemo obrazložiti i dodavanje drugih bridova. Dakle, Kruskalov algoritam radi.

mst5

Implementacija​

Za implementaciju koristimo Union find strukturu i njezine funkcije iz prošle lekcije. Bridove ćemo držati u listi vector<tuple<int, int, int>> edgeList u kojoj je svaki brid između aa i bb težine ww tuple oblika (ww, aa, bb). Tu ćemo listu sortirati po težinama kako bi se algoritam pravilno provodio.

vector<tuple<int, int, int>> mst;
for(auto &edge : edgeList) {
    int a, b;
    tie(ignore, a, b) = edge;

    if(!same(a, b)) {
        mst.push_back(edge);
        unite(a, b);
    }
}
primijetite

Složenost ovog algoritma je O(mlog⁡m)O(m \log m) zbog sortiranja, gdje je mm broj bridova.