Topološko sortiranje

Autor: Martin Josip Kocijan

Uvod

Za neki graf kažemo da je usmjereni (engl. directed) ako je svakom bridu određeno iz kojeg vrha ide u koji vrh. Put (engl. path) je u usmjerenom grafu niz bridova takvih da svaki završava u onom vrhu u kojem sljedeći brid počinje. Ciklus (engl. cycle) jest put u kojem zadnji brid završava u vrhu u kojem počinje prvi brid.

Usmjereni graf možemo topološki poredati ako i samo ako postoji permutacija liste njegovih vrhova, tako da za svaki brid vrijedi da se njegov početni vrh pojavljuje ranije u listi od njegovog završnog vrha. Ako postoji topološki poredak nekog usmjerenog grafa, on ne smije sadržavati nijedan ciklus. U protivnom bismo dobili kontradikciju za prvi i zadnji vrh nekog ciklusa u poretku. S druge strane svakom usmjerenom grafu bez ciklusa možemo pridružiti barem jedan topološki poredak.

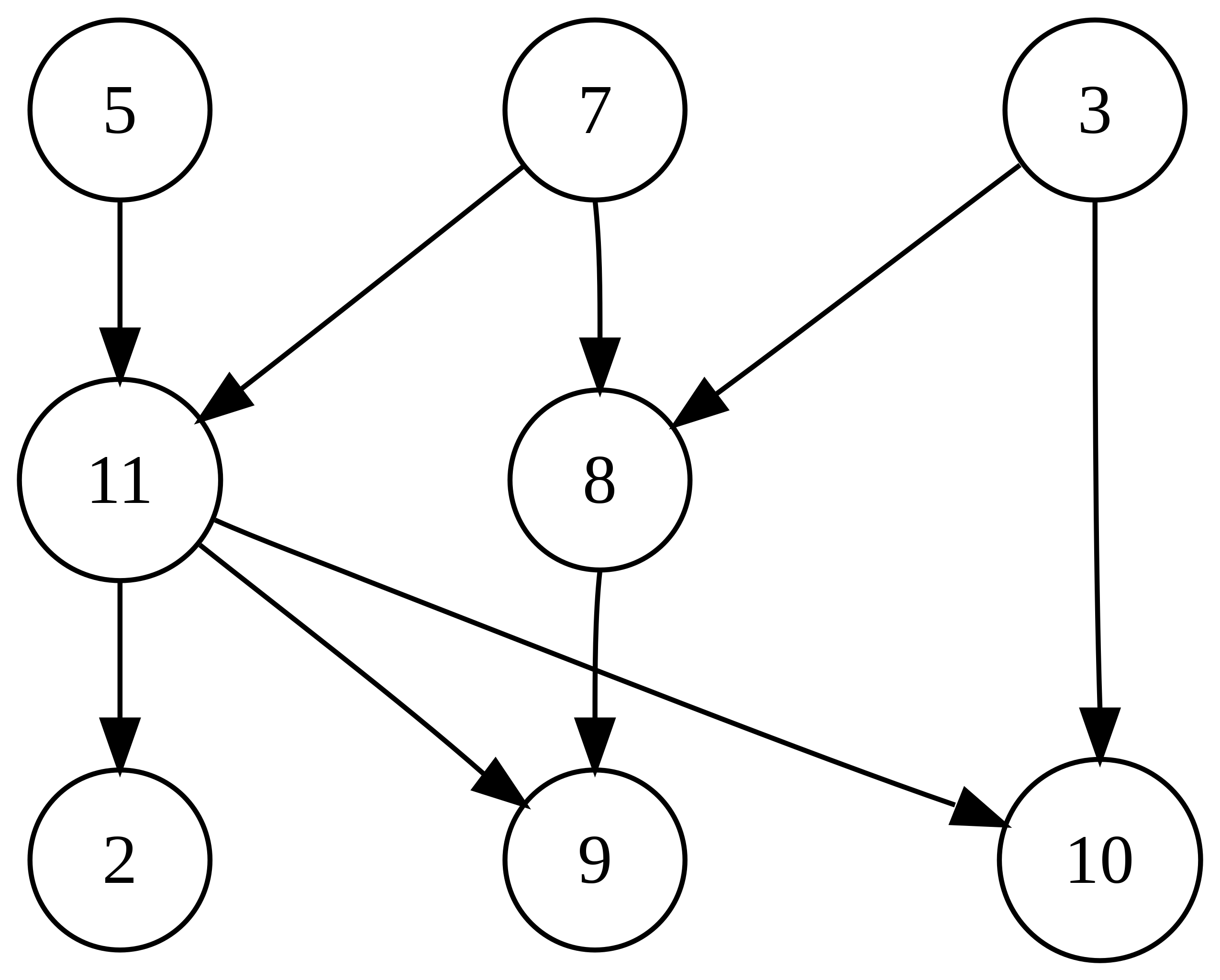
Na slici je neki usmjereni graf bez ciklusa, i za njega postoji puno topoloških poredaka, npr.

• $5$, $7$, $3$, $11$, $8$, $2$, $9$, $10$

Da bismo dobili neki topološki poredak, moramo provesti obilazak grafa tako da neki čvor obrađujemo tek dok smo obradili sve čvorove koji imaju brid prema njemu. Postoje algoritmi DFS i Kahnov algoritam koji to rješavaju. Oba algoritma usput saznaju postoji li uopće topološki poredak. Ako on ne postoji, to je zbog ciklusa kojeg DFS može otkriti.

DFS algoritam

Topološki poredak možemo dobiti tako da okrenemo popis obrađenih čvorova u post-order obilasku svih čvorova DFS-om.

U glavnom programu petljom prolazimo kroz sve čvorove i za svakog rekurzivno pozivamo DFS pretragu. Rekurzivna funkcija završava kad ne može zvati nijedan susjedni čvor koji još nije obrađen. Unutar funkcije zovemo svaki susjedni čvor koji još nismo zvali, te na kraju na početak traženog topološkog poretka zapisujemo trenutni čvor (npr. sa stogom). Ovo nam garantira da, kad zapisujemo neki čvor u listu, svaki čvor koji ovisi o trenutnom čvoru već bude zapisan u listi s desna. Postoje dvije situacije koje su nas dovele do toga. Ili smo do tog ovisnog čvora došli rekurzivno od trenutnog, ili smo rekurzivno obrađivali taj čvor prije nego li smo uopće ušli u trenutni.

Ciklus pronalazimo ako postoji brid iz trenutnog čvora u neki koji je naš trenutni predak (obrada njegove rekurzije još je na stogu). Zato priliskom ulaska u neki čvor njega označujemo kao pozvanog, a prilikom izlaska ga označujemo kao obrađenog. Ako je čvor već pozvan, imamo ciklus i prekidamo algoritam. Ako pak je čvor već obrađen, tada ga samo preskačemo jer je već dodan u rješenje. Svaki čvor posjećujemo samo jednom, pa je algoritam složenosti $O(N+M)$.

void toposort(int cvor) {
    if (pozvana[cvor]) { //ima ciklus
        cout << "Impossible" << endl;
        exit(0);
    }
    // označimo da upravo obrađujemo trenutni čvor
    pozvana[cvor] = 1;
    for (int i = 0; i < graf[cvor].size(); ++i)
        if (!bio[graf[cvor][i]])
            toposort(graf[cvor][i]);
    // označimo da ne moramo opet obraditi trenutni čvor
    bio[cvor] = 1;
    // označimo da smo prestali s obradom trenutnog čvora
    pozvana[cvor] = 0;
    topo.push_back(cvor);
}
// ...
// u funkciji main()
    for (int i = 0; i < n; ++i) {
        if(!bio[i])
            toposort(i);
    }
    // ispišemo topološki poredak
    for (int i = n - 1; i >= 0; --i)
        cout << topo[i] << " ";
    cout << endl;

Kahnov algoritam

Još jedan način da topološki sortiramo vrhove nekog grafa jest Kahnov algoritam. On je sličniji BFS-u nego DFS-u.

Algoritam funkcionira tako da održavamo popis (bilokoja struktura podataka) vrhova koji nemaju nijedan ulazni brid iz nekog vrha kojeg još nismo dodali u rješenje. Na početku se popis sastoji od svih vrhova kojima nemaju nijedan ulazni brid. Uvijek postoji barem jedan takav vrh u svakom nepraznom usmjerenom grafu bez ciklusa. Zatim dodajemo jedan po jedan vrh u s tog popisa na kraj rješenja, i radimo sljedeće za svakog njegovog susjeda v:

• uklonimo brid od u prema v
• ako v nema nijedan drugi ulazni brid, dodajemo ga na popis da ga kasnije možemo obraditi

Ako smo uklonili sve bridove iz grafa, odnosno obradili sve čvorove, pronašli smo neko rješenje. Inače sigurno postoji barem jedan ciklus pa ne postoji nijedno rješenje.

Ovaj algoritam rješenje pronalazi ispravnim redoslijedom pa ga ne moramo okrenuti na kraju kao kad smo koristili DFS.

for (int i = 0; i < n; ++i) {
    for (int j = 0; j < graf[cvor].size(); ++j)
        in_degree[graf[cvor][j]]++;
}
for (int i = 0; i < n; ++i)
    if (in_degree[i] == 0)
        q.push(i);

int cnt;
for (cnt = 0; !q.empty(); ++cnt) {
    // dodamo u rješenje i obradimo neki vrh iz reda
    int u = q.front();
    q.pop();
    topo.push_back(u);

   for (int j = 0; j < graf[u].size(); ++j)
        // uklanjamo izlazni brid iz trenutnog vrha tako da ulazni stupanj svakog njegovog susjeda smanjimo za 1
        --in_degree[graf[u][j]];
        // ako ne postoji nijedan drugi ulazni brid prema susjedu možemo ga obraditi
        if (in_degree[graf[u][j]] == 0)
            q.push(graf[u][j]);
        // primjetimo da kad tražimo neki vrh koji je ulaznog stupnja 0, dovoljno je održavati popis takvih vrhova koji potencijalno ažuriramo samo onda kada obrađujemo neki vrh koji ulazi u njih
}

if (cnt < n) { // ima ciklus
    cout << "Impossible" << endl;
    exit(0);
}
// ispišemo topološki poredak
for (int i = 0; i < n; ++i)
    cout << topo[i] << " ";
cout << endl;

Najkraći putevi

Ako nas zanimaju najkraći putevi od nekog vrha do svakog drugog vrha u usmjerenom grafu bez ciklusa, možemo koristiti topološko sortiranje. Ako graf ima $N$ vrhova i $M$ bridova, postići ćemo linearnu složenost od $O(N + M)$, umjesto Dijkstrine složenosti od npr. $O(M \log M)$.

for (int i = 0; i < n; ++i) {
    dist[i] = 0x3f3f3f3f; // ili 1e9
}
dist[pocetni_vrh] = 0;
for (int i = 0; i < n; ++i) {
    int u = topo[i];
    for (int j = 0; j < graf[u].size(); ++j) {
        if (dist[graf[u][j]] > dist[u] + graf_dist[u][j])
            dist[graf[u][j]] = dist[u] + graf_dist[u][j];
    }
}

Hamiltonov put

Općenito je problem pronalaženja Hamiltonovih puteva u usmjerenim grafovima nemoguće riješiti u polinomskoj složenosti. U slučaju kada ne postoji nijedan ciklus, moguće je taj problem riješiti u čak linearnoj složenosti. Opet koristimo topološko sortiranje, te promatramo je li ono jedinstveno. Naime, dovoljno je provjeriti postoji li brid između svaka dva susjedna vrha u topološkom poretku. Ako je tako, topološki je poredak jedinstven te taj niz bridova čini Hamiltonov put u grafu. Ako pak su neka dva vrha susjedna u topološkom poretku ali između njih ne postoji brid, tada ih možemo zamijeniti. Dobit ćemo još jedan valjan topološki poredak, pa zaključujemo da on nije jedinstven.