2SAT

Autor: Martin Josip Kocijan

Notacija

$\lnot$ jest logička operacija NOT (NE).

$\land$ jest logička operacija AND (I).

$\lor$ jest logička operacija OR (ILI).

$\equiv$ ili $\iff$ označava logičku ekvivalenciju.

$\Longrightarrow$ predstavlja logičku implikaciju.

Uvod

SAT (Boolean satisfiability problem) jest problem pridruživanja istine ili laži varijablama tako da se zadovolji neka Booleova funkcija zapisana u kanonskom obliku produkta maksterma. To se preciznije naziva konjunktivna normalna forma.

2-SAT poseban je slučaj SAT-a kada se svaki maksterm sastoji od dvije varijable.

$$\begin{aligned} &(x_0\lor x_2)\land(x_0\lor\lnot x_3)\land(x_1\lor\lnot x_3)\land(x_1\lor\lnot x_4)\land{} \\ &(x_2\lor\lnot x_4)\land{}(x_0\lor \lnot x_5)\land (x_1\lor\lnot x_5)\land (x_2\lor\lnot x_5)\land{} \\ &(x_3\lor x_6)\land (x_4\lor x_6)\land (x_5\lor x_6) \end{aligned}$$

Iznad je napisan primjer funkcije koju je potrebno zadovoljiti. Cilj nam je dodijeliti varijablama $x_i$ vrijednosti istinu ili laž, tako da izraz naposljetku bude istinit. Primjetimo da to znači da u svakoj zagradi barem jedan operand operacije $ili$ mora biti istinit. Ako je taj operand oblika $x_i$, tada mora vrijediti $x_i = 1$. Ako pak je taj operand oblika $\lnot x_i$, onda mora biti $x_i = 0$.

Znamo:

$$(x_0\lor\lnot x_3) \;\equiv\; (\lnot x_0\Rightarrow\lnot x_3) \;\equiv\; (x_3\Rightarrow x_0)$$

Dakle možemo konstruirati usmjereni graf s po dva vrha za svaku varijablu: jedan za nju samu, i još jedan za njezin komplement. Povlačimo brid iz jednog vrha u drugi kada vrijednost prvog vrha implicira vrijednost drugog vrha u zadanoj formuli. Na donjoj je slici konstruiran takav graf za gore navedeni primjer.

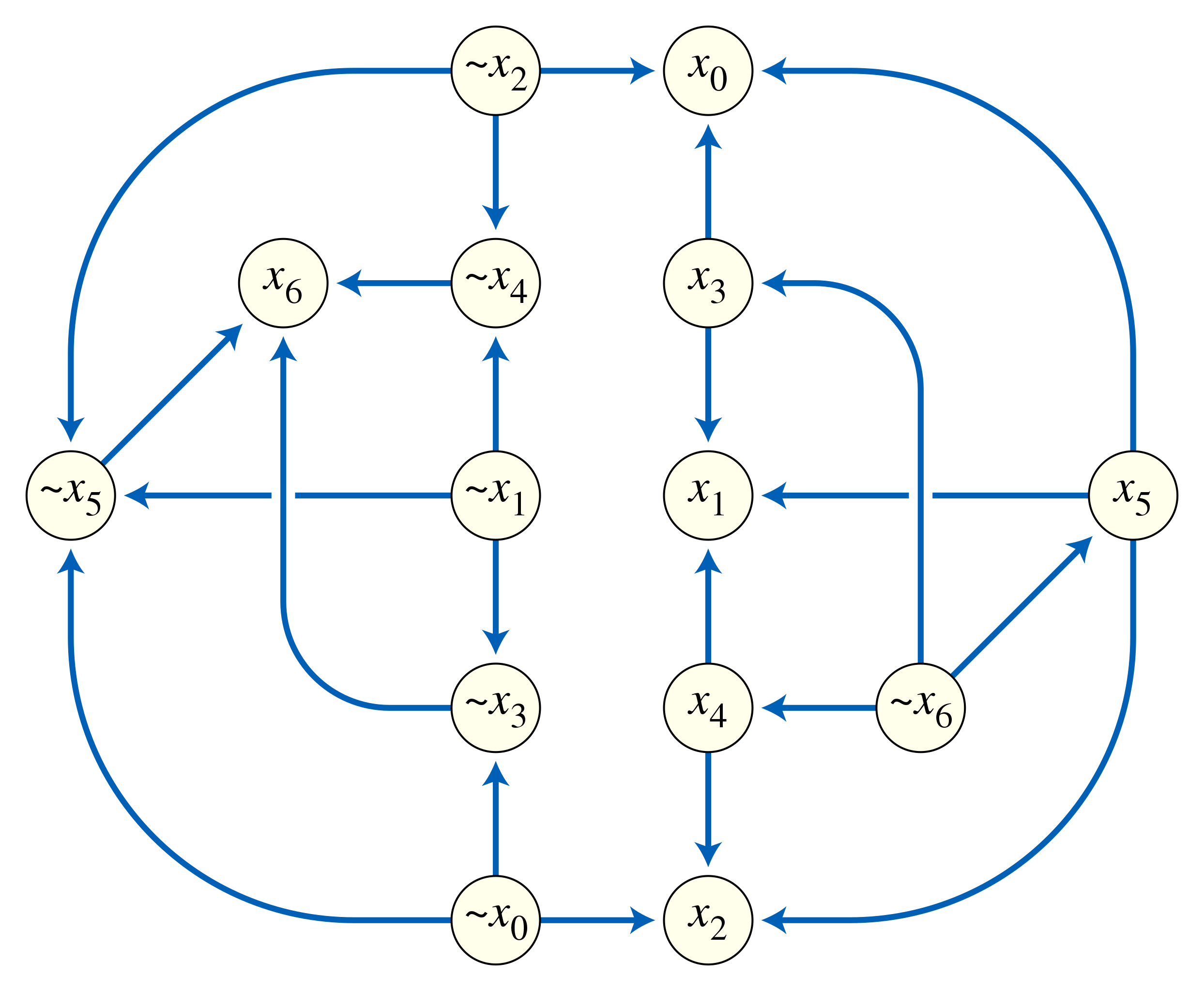
Rješenje

2SAT problem ima rješenje ako i samo ako njegov zapis kao gore definirani graf s implikacijama nema $x_i$ i $\lnot x_i$ u istoj strogo povezanoj komponenti, za svaku varijablu $x_i$.

U protivnom postoji barem jedno rješenje, koje je moguće dobiti sljedećim postupkom:

• Konstruiramo usmjereni graf $G$ kao što je gore opisano
• Odredimo strogo povezane komponente grafa
• Kondenziramo graf, odnosno u $G$ svaku strogo povezanu komponentu stegnemo da dobijemo $G'$, u kojem svaki vrh predstavlja jednu strogo povezanu komponentu iz $G$. U grafu $G'$ postoji brid iz $u'$ u $v'$ ako postoji brid $uv$ u $G$ takav da je $u \in u'$ i $v \in v'$.
• Topološki sortiramo vrhove u $G'$ i rješenje zapišemo u neku listu $L$
• Obrnutim redoslijedom prolazimo kroz $L$ i obrađujemo komponentu po komponentu:
  • Svi vrhovi u komponenti moraju biti iste logične vrijednosti, znači ili su svi istiniti ili su svi lažni.
  • Ako barem jedan vrh nema pridruženu logičnu vrijednost, tada ćemo svim vrhovima u komponenti pridružiti istinu. Ako u nekom vrhu piše $x_i$, postavljamo $x_i = 1$. Ako pak u nekom vrhu piše $\lnot x_i$, tada postavljamo $x_i = 0$. Time postižemo da je svaki vrh u komponenti istinit, pa ne može doći do lažne implikacije $1 \Rightarrow 0$.
  • Ovo smo radili obrnutim topološkim redoslijedom jer, ako postoji put od komponente $X$ do komponente $Y$, želimo prvo postaviti komponentu $Y$ da bude istinita. Ovime sprječavamo da dođe do lažne implikacije $1 \Rightarrow 0$.