LCA

Autor: Martin Josip Kocijan

Uvod

Nekad funkcije možemo zapisati pomoću usmjerenih grafova. Tada svaki vrh ima izlazni stupanj točno 1. Ako ne postoji nijedan ciklus duljine veće od 1, postojat će barem jedna petlja. Prvi nasljednik nekog vrha definiramo kao jedini njemu susjedan vrh. Možemo napraviti kompoziciju funkcije, pa nas tako zanima drugi nasljednik, treći nasljednik, pa čak i $10^{18}$-ti nasljednik. Rješenje je da iterativno izračunamo svaki $2^n$-ti nasljednik. Tada brzim potenciranjem možemo izračunati svaki $m$-ti nasljednik u složenosti $O(\log m)$.

Problem

Ako je stablo ukorijenjeno, za svaki vrh postoji točno jedan vrh koji nazivamo njegovim roditeljem. Za korijen stabla možemo reći da nema korijen, ili kažemo da je on sam sebi roditelj. Predak nekog vrha definiramo ovako:

• ako je vrh x roditelj vrha y, tada kažemo i da je x (prvi) predak od y
• ako je vrh x ($n$-ti) predak vrha y, a y je roditelj vrha z, tada je vrh x ($n+1$-ti predak) vrha z

Svaka dva vrha imaju zajedničke podskupove predaka, tj. za svaka dva vrha u i v postoji njima zajednički predak x takav da je svaki predak od x ujedno i predak od u i v.

Želimo za neka dva vrha saznati koji im je najniži zajednički predak (engl. lowest common ancestor, LCA) u stablu, odnosno koji im je zajednički predak najudaljeniji od korijena stabla.

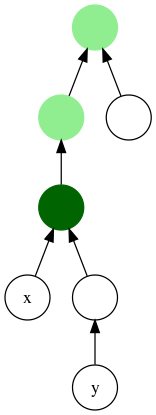
Na slici je tamno zeleno obojan najniži zajednički predak vrhova x i y. Svijetlo zeleni vrhovi predstavljaju zajedničke predke vrhova x i y koji nisu najniži.

Primjena

Za svaka tri vrha x, y i z u nekom grafu G postoji vrh m takav da je on sadržan u svakom putu između neka dva vrha među x, y i z. Ako imamo neke x, y i z, možemo izračunati lca(x,y), lca(x,z), lca(y,z) i lca(x,lca(y,z)). Barem tri od njih bit će isti vrh. Također vrijedi lca(x,lca(y,z)) == lca(y,lca(x,z)) == lca(z,lca(x,y)).

Neka smo za svaki vrh izračunali njegovu dubinu, odnosno njegovu udaljenost od korijena. Označimo dubinu vrha x sa dep[x]. Tada je udaljenost nekog vrha x od vrha y jednaka: dep[x] + dep[y] - 2 * dep[lca(x,y)].

Rješenje u logaritamskoj složenosti

Dovoljno je za svaki vrh izračunati njegov $2^i$-ti predak, za svaki nenegativni cijeli broj $i$ manji ili jednak $\log_{2}n$, gdje je $n$ broj vrhova u grafu. Reći ćemo da je korijen sam sebi roditelj.

Algoritam je opisan u donjem kodu.

#include <iostream>
using namespace std;

const int N = 1e5;
const int LOG = 22;

int n;
// a[i][j] pamti 2^i-ti predak od j
// a[0][j] predstavlja roditelja od j
int a[LOG][N];
int dep[N];

// lca(u, v) == lca(v, u)
int lca(int u, int v)
{
  if (dep[u] < dep[v]) swap(u, v);
  // sada je sigurno dep[u] >= dep[v]

  // ako u i v nisu na istoj razini (udaljenosti od korijena), tada je x-ti predak od u jednak x-tom predku od v samo ako se radi o korijenu
  for (int i = LOG - 1; i >= 0; i--) {
    // svaki broj ima jedinstveni binarni zapis
    // dižemo vrh u na istu razinu kao što je vrh v
    // to jest, dižemo vrh u za dep[u] - dep[v] razina
    if (dep[a[i][u]] >= dep[v])
      u = a[i][u];
  }

  // dva vrha se nikada ne podudaraju ako nisu na istoj razini
  // dep[lca(u,v)] <= min(dep[u], dep[v])
  // ako smo dizanjem u do razine s v dobili da su u i v isti vrh, ispišemo ga, to nam je traženi LCA
  // ovo se dešava kada je u predak od v, ili je v predak od u
  if (u == v) return u;

  // dižemo u i v na istu razinu čim bliže korijenu, ali dokle god nisu isti
  for (int i = LOG - 1; i >= 0; i--) {
    if (a[i][u] != a[i][v]) {
      u = a[i][u];
      v = a[i][v];
    }
  }
  
  // maksimalno smo digli u i v na istu razinu bez da su isti
  // slijedi da su roditelji od u i v isti
  // a[0][u] = a[0][v], pa nam je svejedno koji vratimo, to je traženi LCA
  return a[0][u];
}

int main()
{
  scanf("%d", &n);
  // 2^0=1-ti predak od korijena je on sam
  a[0][1] = 1;
  // dubina nekog cvora je njegova udaljenost od korijena + 1
  dep[1] = 1;
  for (int i = 1; i <= n; i++) {
    int m;
    // čvor i ima m djece
    scanf("%d", &m);
    for (int j = 0; j < m; j++) {
      int ch;
      // unosimo dijete od čvora i
      scanf("%d", &ch);
      // roditelj čvora ch jest i
      a[0][ch] = i;
      // ch je za 1 udaljeniji od korijena nego i
      dep[ch] = dep[i] + 1;
    }
  }
  // pretprocesiramo matricu predaka
  for (int i = 1; i < LOG; i++) {
    // obavezno mora biti ovo iznad vanjska petlja a ovo ispod unutarnja
    for (int j = 1; j <= n; j++) {
      // ovo je ključno
      // 2^i-ti predak od j jest 2^(i-1)-ti predak od 2^(i-1)-tog predka od j
      a[i][j] = a[i - 1][a[i - 1][j]];
    }
  }
  int q;
  // postavljamo q upita o najnižim zajedničkim predcima
  scanf("%d", &q);
  for (int i = 0; i < q; i++) {
    int u, v;
    // zanima nas najniži zajednički predak vrhova u i v
    scanf("%d%d", &u, &v);
    // ispisujemo lca(u, v) koja ga računa
    printf("%d\n", lca(u, v));
  }
  return 0;
}