Kosarajuev algoritam

Autor: Martin Josip Kocijan

Definicija

Za neki usmjereni graf kažemo da je strogo povezan (engl. strongly connected) ako postoji put između svaka dva vrha. Ako su u i v različiti vrhovi, tada postoji put od u do v te postoji put od v do u.

Usmjerene grafove možemo rastaviti na disjunktne strogo povezane komponente (engl. strongly connected components) gdje je svaka komponenta neki podgraf koji je strogo povezan.

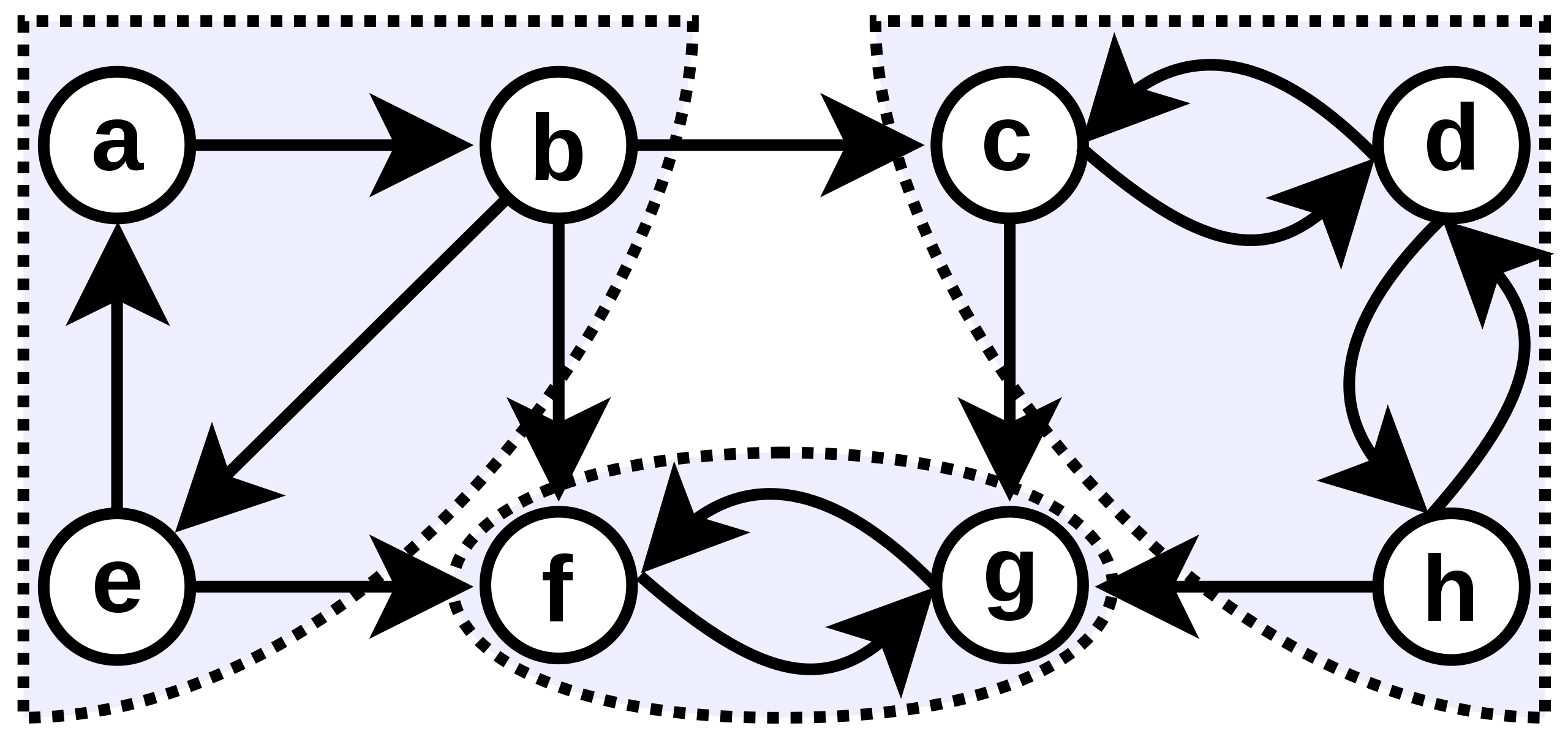
Na slici je primjer usmjerenog grafa kojem su označene njegove strogo povezane komponente. One su $\{a, b, e\}$, $\{c, d, h\}$ i $\{f, g\}$.

Algoritam

Kosarajuev algoritam započinje topološkim sortiranjem vrhova usmjerenog grafa. Nakon toga pronalazimo strogo povezane komponente.

Potrebno je napisati dva DFS-a. Prvi služi za generiranje topološkog poretka koji spremamo u neku listu. Zatim prvo promijenimo smjer svim bridovima u grafu. Prema prethodno dobivenom topološkom poretku nekom čvoru x u njegovu komponentu rekurzivno pridružujemo sve čvorove do kojih postoji put od x. Preciznije, u glavnom programu petljom prolazimo po svim čvorovima u prema topološkom poretku. Za svaki čvor u zovemo dfs2(u, u). Rekurzija dfs2(x, y) prvo provjerava je li čvoru x već obrađen, odnosno je li mu već pridružena neka komponenta. Ako nije, čvor x pridružuje se onoj komponenti u kojoj je već y. Nakon toga u rekurziji prolazimo petljom po svim susjedima v od x te zovemo dfs2(v, y).

Algoritam je linearne složenosti, odnosno $O(N+M)$.

Implementacija

#include <iostream>
#include <stack>
#include <vector>
#include <cstring>
using namespace std;
#define N 200200
 
int n, m;
int u, v;
vector<int> g[N];
// ako imamo matricu susjedstva, možemo dobiti inverz i tako da ju transponiramo
vector<int> g_inv[N];
int bio[N];
stack<int> topo;
// ovdje zapisujemo rješenje, tako da su dva vrha x i y u istoj komponenti ako je comp[x] == comp[y]
// mogli smo rješenje zapisati i u bio[] samo treba paziti na brojeve koji označavaju komponente i broj koji označava neposjećeni čvor
int comp[N];
 
void dfs1(int cv)
{
  if (bio[cv]) return;
  bio[cv] = 1;
  for (int i: g[cv]) {
    dfs1(i);
  }
  topo.push(cv);
}
 
void dfs2(int cv, int root)
{
  if (bio[cv]) return;
  bio[cv] = 1;
  // comp[cv] = comp[root]
  comp[cv] = root;
  // svim bridovima trebamo zamijeniti smjer pa nas ne zanimaju izlazni nego ulazni bridovi
  for (int i: g_inv[cv]) {
    dfs2(i, root);
  }
}
 
int main()
{
  scanf("%d%d", &n, &m);
  for (int i = 0; i < m; i++) {
    scanf("%d%d", &u, &v);
    // zapisujemo da čvor u ima izlazni brid prema v
    g[u].pb(v);
    // zapisujemo da čvor v ima ulazni brid iz u
    g_inv[v].pb(u);
  }
  for (int i = 0; i < n; i++) {
    dfs1(i);
  }
  // možemo reciklirati polje bio[]
  memset(bio, 0, sizeof bio);
  for (int i = 0; i < n; i++) {
    int cv = topo.top();
    topo.pop();
    dfs2(cv, cv);
  }
  // za svaki čvor ispisujemo kojoj komponenti on pripada
  // vrijedi comp[x] == comp[y] ako i samo ako se x i y nalaze u istoj strogo povezanoj komponenti
  for (int i = 0; i < n; i++) {
    printf("%d\n", comp[i]);
  }
  return 0;
}

Odnosi između strogo povezanih komponenata

Svaki usmjereni graf možemo kondenzirati u usmjereni graf bez ciklusa tako da svaku njegovu strogo povezanu komponentu stegnemo u jedan vrh.

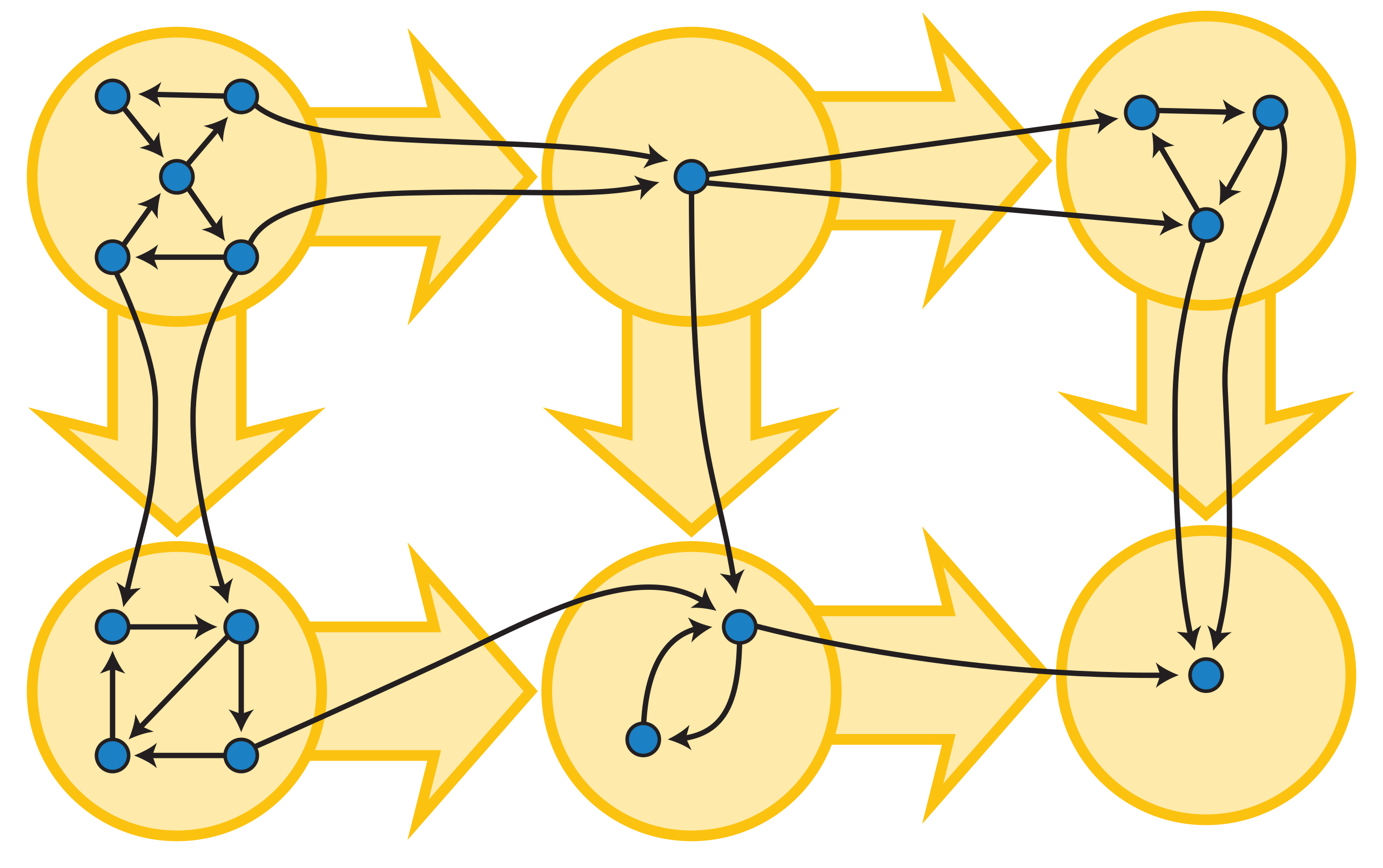
Na slici je primjer kondenzacije plavog usmjerenog grafa u žuti. Dok plavi ima cikluse, žuti ih nema. Svaka strogo povezana komponenta plavog grafa predstavljena je jednim žutim vrhom. Ako iz nekog vrha u jednoj plavoj komponenti postoji brid prema nekom vrhu u drugoj komponenti, postoji i brid između odgovarajućih žutih vrhova.

for (int i = 0; i < n; i++) {
    for (int j: g[i]) {
      if (comp[i] != comp[j]) {
        printf("Postoji brid iz cvora %d komponente %d prema cvoru %d komponente %d\n", i, comp[i], j, comp[j]);
      }
    }
  }