Najkraći putovi

Autor: Maja Milas

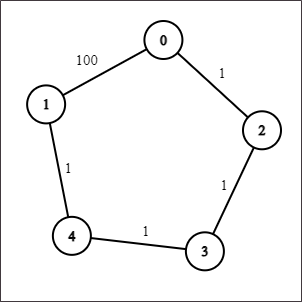
Traženje najkraćeg puta između dva vrha grafa čest je problem s puno praktičnih primjena. U netežinskim grafovima duljina najkraćeg puta odgovara broju bridova između dva odabrana vrha. Da bi pronašli takav put, dovoljno je pustiti BFS iz početnog čvora i odmah dobivamo rješenje. Ako je graf težinski, stvar se malo komplicira što možete vidjeti na slici ispod. BFS bi za zadani graf rekao da je najkraći put između 0 i 1 duljine 100, a mi odmah vidimo da to nije istina. Kako bi znali riješiti i ovakve probleme, pogledat ćemo nekoliko algoritama za najkraći put na težinskim grafovima.

Bellman-Ford

Bellman-Ford algoritam pronalazi duljinu najkraćeg puta od nekog početnog vrha do svih ostalih vrhova u grafu. Algoritam radi na svim tipovima grafova pod uvjetom da nemaju ciklus s negativnom sumom težina. Ako u grafu postoji ciklus s negativnom težinom, ovaj algoritam to može detektirati.

Algoritam za svaki vrh pamti njegovu udaljenost od početnog. Na početku znamo samo da je udaljenost od početnog do početnog nula, a sve ostale postavljamo na beskonačno. U svakom koraku pokušavamo popraviti te udaljenosti tako što prolazimo po listi bridova i provjeravamo može li se smanjiti udaljenost ako iskoristimo trenutni brid. Postupak ponavljamo dok udaljenosti nisu konačne.

Kako radi?

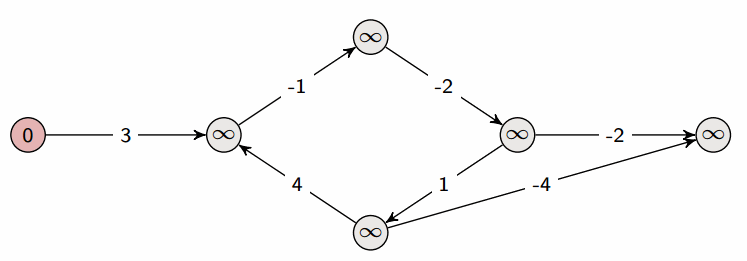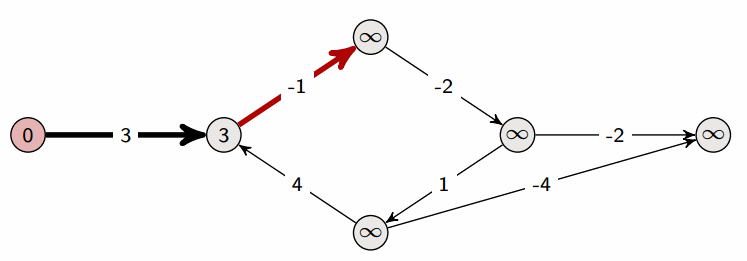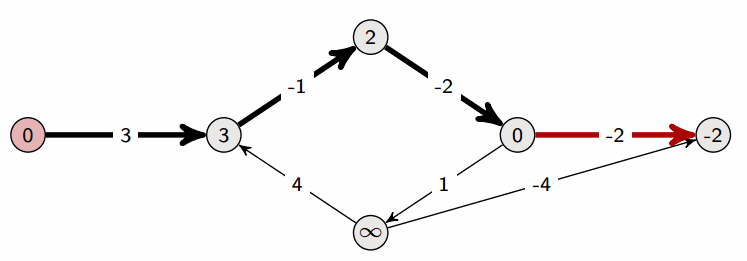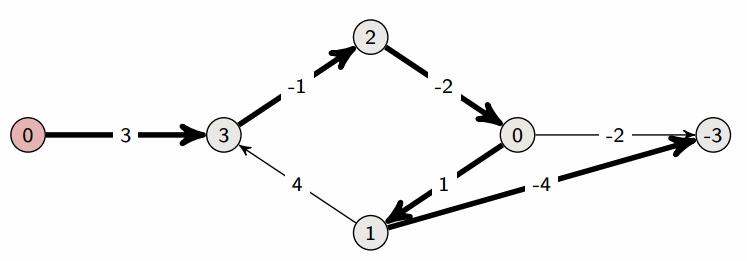
Napravimo polje distance u kojem na poziciji distance[i] piše kolika je udaljenost od početnog do i-tog vrha i postavimo sve udaljenosti na $\infty$ (čitaj: neki ogroman broj). Cilj nam je smanjivati te udaljenosti tako da na kraju u distance[i] piše duljina najkraćeg puta do i-tog vrha. Označimo početni vrh slovom $p$ i postavimo udaljenost do njega na nulu. Na slici ispod je početni vrh 1, a crvenom su bojom napisane vrijednosti u polju distance.

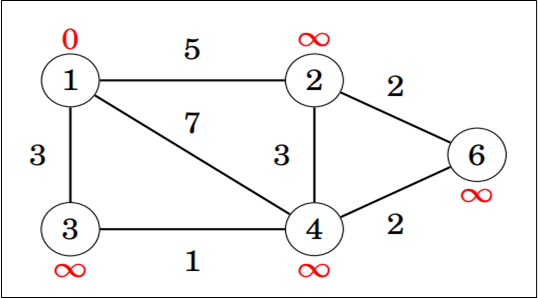
Sada iteriramo po bridovima. Za svaki brid između $a$ i $b$ težine $w$ provjeravamo možemo li pomoću njega smanjiti udaljenost od početnog vrha. Odnosno, za brid (a, b, w) radimo distance[b] = min(distance[b], distance[a]+w).

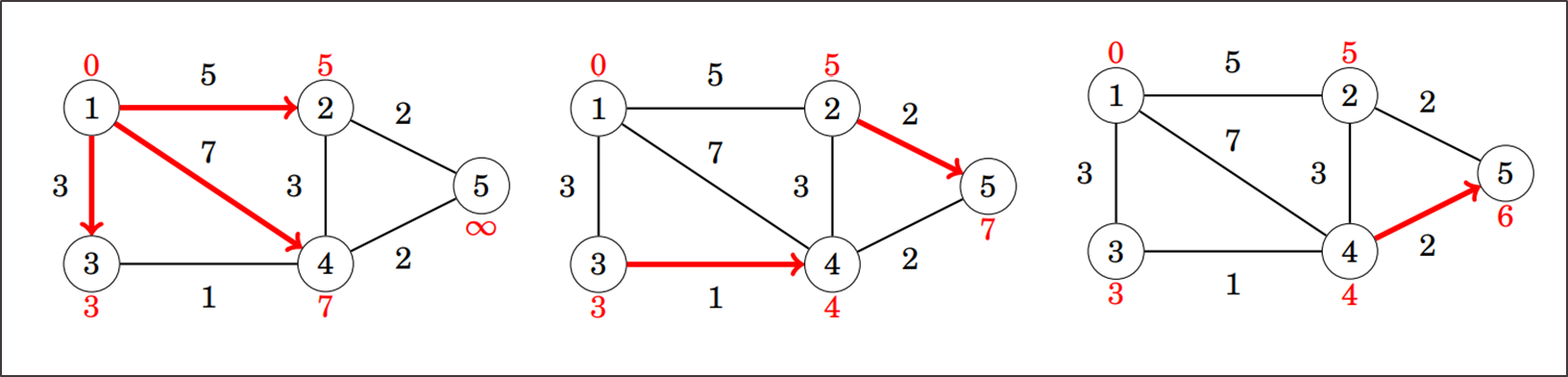
Na slici vidimo (više-manje) redoslijed prolaska kroz bridove te kako se polje distance mijenja kada dodamo novi brid. U ovom smo primjeru bridove birali takvim redoslijedom da nakon samo jednog prolaska kroz sve imamo dobro napisane najkraće puteve. U praksi će redoslijed bridova biti nasumičan pa ćemo morati više puta ponoviti cijeli postupak dok ne dobijemo točne udaljenosti. Zato ćemo u kodu prolazak po bridovima ponavljati $n-1$ puta (n je broj vrhova u grafu) jer svaki najkraći put može sadržavati maksimalno $n-1$ brid pa će to uvijek biti dovoljno.

Ako je još nešto ostalo zbunjujuće, bacite oko na ovaj simpa gif sa kjaer.io:

Implementacija

U sljedećoj je implementaciji graf spremljen kao lista bridova s težinama (vector<tuple<int,int,int>> edgeList).

//INF je neki veliki broj, p je pocetni vrh
for(int i=0; i<n; i++) distance[i] = INF;
distance[p] = 0;

for(int i=0; i<n-1; i++) {
    for(auto e : edgeList) {
        int a, b, w;
        tie(a, b, w) = e; // "raspakira" tuple u a, b i w
        distance[b] = min(distance[b], distance[a]+w);
    }
}

primijetite

Složenost ovog algoritma je $O(n*m)$, gdje je $n$ broj vrhova, a $m$ broj bridova.

Negativan ciklus

Ako u grafu postoji ciklus kojemu je suma težina negativna, ne možemo dobro definirati najkraći put između dva čvora zato što ćemo uvijek moći još jednom obići ciklus i smanjiti ukupan put. Ako nakon $n-1$ koraka i dalje možemo popraviti put do nekog čvora, to nam govori da graf ima negativan ciklus.

Dijkstrin algoritam

Dijkstrin algoritam, kao i Bellman-Ford, pronalazi duljine najkraćih puteva od početnog vrha do svih ostalih. Prednost ovog algoritma je što je brži od Bellman-Forda pa ga možemo koristiti i na većim grafovima. Njegov nedostatak je što zahtijeva da graf nema bridove negativne težine što nije bio uvjet za Bellman-Ford.

Ideja algoritma je slična BFS-u jer u svakom koraku obrađujemo jedan vrh i dodajemo u red njegove susjede koji još nisu obrađeni. Razlika je u tome što će ovoga puta vrh koji idući obrađujemo uvijek biti onaj koji trenutno ima najmanju udaljenost od početnog. Na taj ćemo način riješiti problem s početka lekcije.

Ako si malo zaboravio/la BFS, ovo je odličan trenutak da se podsjetiš prije nego nastaviš dalje. 😄

Kako radi?

Ponovno koristimo polje distance analogno onom ranije te mu na isti način incijaliziramo vrijednosti prije provođenja algoritma. Početni vrh je 1 pa smo postavili udaljenost do njega na nulu.

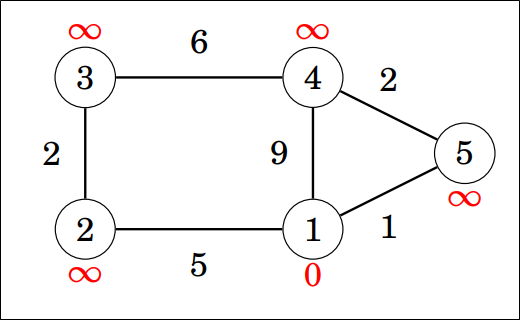
U svakom koraku biramo neobrađeni vrh s najmanjom udaljenosti od početnog (trenutno najbliži vrh) te pokušavamo smanjiti udaljenost do svih njegovih susjeda.

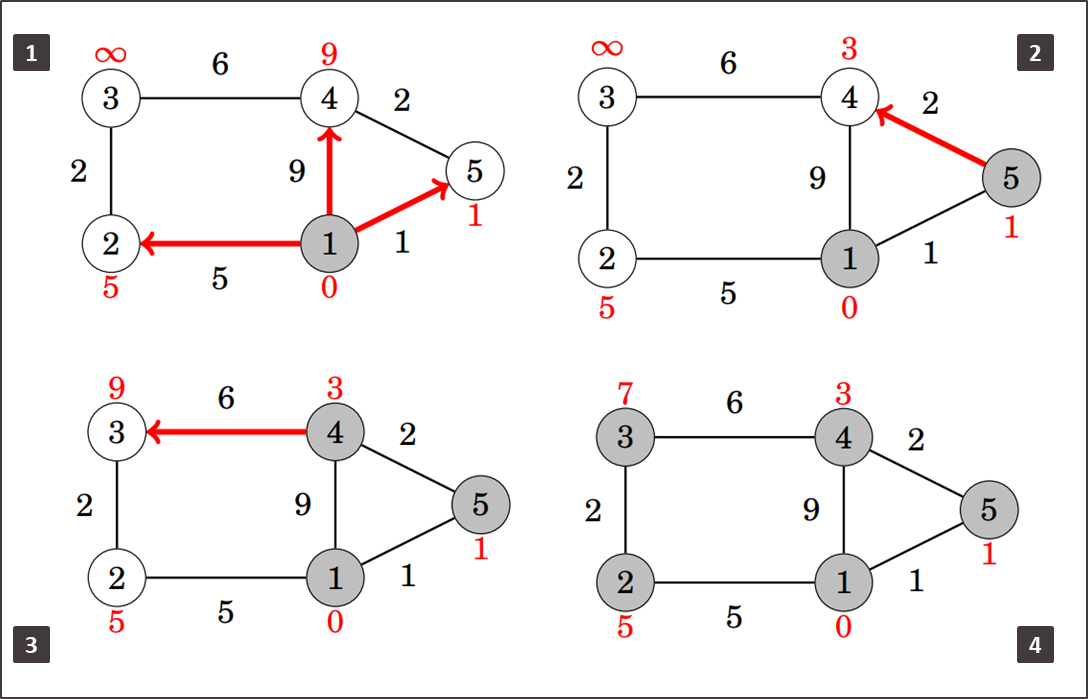
U prvom je koraku najbliži vrh 1 pa njega obrađujemo i popravljamo udaljenosti do njegovih susjeda koje potom dodajemo u red. U drugom koraku ćemo ponovno birati najbliži vrh, a to će sada biti 5 jer smo njegovu udaljenost popravili na 1 (ostale udaljenosti su 9 i 5). Postupak se nastavlja na isti način dok ne posjetimo sve vrhove. Dobra stvar kod ovog algoritma je što svaki vrh obrađujemo samo jednom i nakon toga ga ne moramo više provjeravati.

Implementacija

Da bi algoritam bio efikasan, moramo na brz način moći doći do trenutno najbližeg neobrađenog vrha. Bilo bi super kada bismo red koji nam služi za praćenje vrhova imali u nekoj strukturi koja nam odmah vraća najbliži. Nakon malo kopanja po moždanoj arhivi, sjetit ćete da bi za ovo priliku mogli koristiti prioritetni red (priority_queue) koji drži elemente sortiranima i osigurava njihovo dodavanje u logaritamskoj složenosti (dakle, jako brzo). Budući da prioritetni red omogućava pristup najvećem elementu, u njega ćemo spremati parove $(-d, x)$ gdje $d$ označava trenutnu udaljenost vrha $x$. Vrh s najmanjim $d$ će tada biti najmanje negativan i uzet ćemo ga s vrha reda.

U sljedećoj je implementaciji graf spremljen kao vector<vector<pair<int,int>>> adjList, odnosno kao lista susjedstva gdje je uz vrh napisana i težina brida. Početni vrh je $p$. Koristimo i polje processed u kojem zapisujemo jesmo li već posjetili neki vrh.

for(int i=0; i<n; i++) distance[i] = INF;
distance[p] = 0;
q.push({0, p});

while(!q.empty()) {
    int a = q.top().second;
    q.pop();

    if(processed[a]) continue;
    processed[a] = true;

    for(auto u : adjList[a]) {
        int b = u.first, w = u.second;
        if(distance[a]+w < distance[b]) {
            distance[b] = distance[a] + w;
            q.push({-distance[b], b});
        }
    }
}

primijetite

Složenost ovog algoritma je $O(n+m*\log{m})$ jer algoritam prolazi kroz sve vrhove i za svaki brid u priority_queue doda najviše jedan par.

Floyd-Warshall

Floyd-Warshall algoritam za razliku od prethodna dva traži najkraći put između svaka dva vrha grafa. Iz tog razloga ovoga puta koristimo 2D matricu distance[i][j] u kojoj su zapisane udaljenosti među vrhovima. Na početku zaisujemo samo udaljenosti vrhova između kojih postoji brid, a ostale postavljamo na beskonačno. Kasnije kombinacijom bridova popravljamo i ostale udaljenosti dok ne dobijemo točno rješenje.

Kako radi?

Pogledajmo kako radi algoritam na sljedećem grafu:

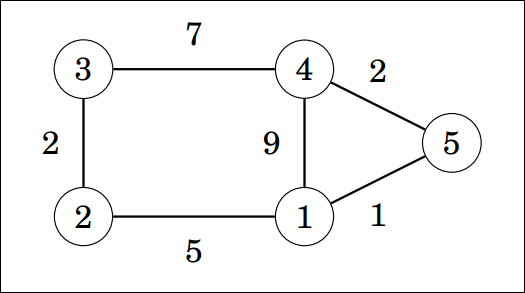
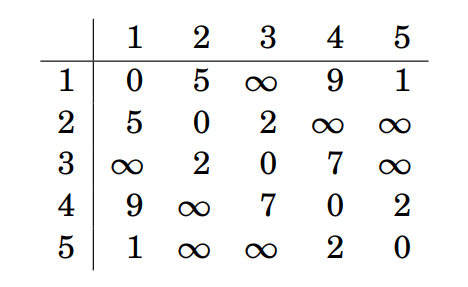
Prvo napravimo matricu udaljenosti na sljedeći način:

• distance[i][j]=0 ako je i=j
• distance[i][j]=w ako postoji brid između vrhova i i j
• distance[i][j]=INF ako ne postoji brid između vrhova i i j

Pri svakom koraku algoritam bira jedan vrh te preko njega pokušava popraviti udaljenosti do svih ostalih. Ako popravljamo udaljenosti pomoću nekog vrha $x$, za svaka dva čvora $a$ i $b$ se pitamo je li bolja vrijednost distance[a][b] (njihova trenutna udaljenost) ili je bolje da idemo preko vrha $x$, odnosno distance[a][x] + distance[x][b]?

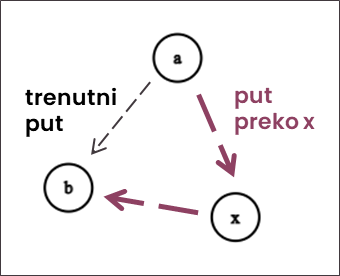
Implementacija

Ovaj je algoritam poznat po jednostavnoj implementaciji. Polje distance inicijaliziramo s dvije petlje prema uputama gore i potom računamo najkraće udaljenosti:

for (int k=1; k<=n; k++) {
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=n; j++) {
            // popravljanje udaljenosti i-j preko vrha k
            distance[i][j] = min(distance[i][j], distance[i][k]+distance[k][j]);
        }
    }
}

primijetite

Vremenska složenost ovog algoritma je $O(n^3)$ (ugniježđene petlje), a prostorna $O(n^2)$.

Usporedba algoritama

	Bellman-Ford	Dijkstra	Floyd-Warshall
duljina najkraćeg puta	od početnog vrha do svih ostalih	od početnog vrha do svih ostalih	između svih parova vrhova
nedostatci	ne radi ako ima negativan ciklus	ne radi ako postoje bridovi negativne težine	prostorna složenost $O(n^2)$
vremenska složenost	$O(nm)$	$O(n+m\log m)$	$O(n^3)$