Fenwickovo stablo
Uvod
Fenwickovo stablo je struktura podataka koja omogućuje upite sumom prefiksa niza i promjenu vrijednosti elementa niza, sve u . Fenwickovo stablo je još poznato pod imenom binarno indeksirano stablo, iako zapravo nije ni stablo, već niz.
Prije nego što objasnimo strukturu, upoznajmo se sa sljedećom operacijom.
Izoliranje posljednjeg postavljenog bita
Kao što naslov kaže, potrebno je iz nekog broja uzeti posljednji postavljeni bit, dakle bit čija je vrijednost 1.
Npr, imamo broj 14. Ako ga prikažemo u bazi 2, on izgleda ovako: 0000 1110
Ako izoliramo posljednji postavljeni bit, dobijemo 2 (0000 0010), a to se postiže bitovnom operacijom s dvojnim komplementom broja. Brzo rješenje je sljedeće:
Ova operacija je vrlo bitna za Fenwickovo stablo.
Struktura
Svaki indeks u Fenwickovom stablu predstavlja sumu intervala , gdje predstavlja posljednji postavljeni bit u indeksu . Koristit ćemo 1-indeksiranje kod nizova.
Primjer:
Neka je početak intervala, a kraj intervala.
| Indeks | bitovni prikaz | interval | ||
|---|---|---|---|---|
| 1 | 0001 | 1 | ||
| 2 | 0010 | 2 | ||
| 3 | 0011 | 1 | ||
| 4 | 0100 | 3 | ||
| 5 | 0101 | 1 | ||
| 6 | 0110 | 2 | ||
| 7 | 0111 | 1 | ||
| 8 | 1000 | 4 |
Kako sad iz ovoga izračunati sumu prefiksa niza?
Uzet ćemo indeks 7 kao primjer. On predstavlja sumu intervala . Ako od njega oduzmemo posljednji postavljeni bit (1), dobijemo indeks 6, tj. interval . Od broja 6 oduzmemo njemu posljednji postavljeni bit (2). Dobijemo indeks 4 ili interval .
Imamo sljedeće intervale: , , . Njihovom unijom dobijemo interval što predstavlja sumu prefiksa niza za indeks 7.
Ilustracija:
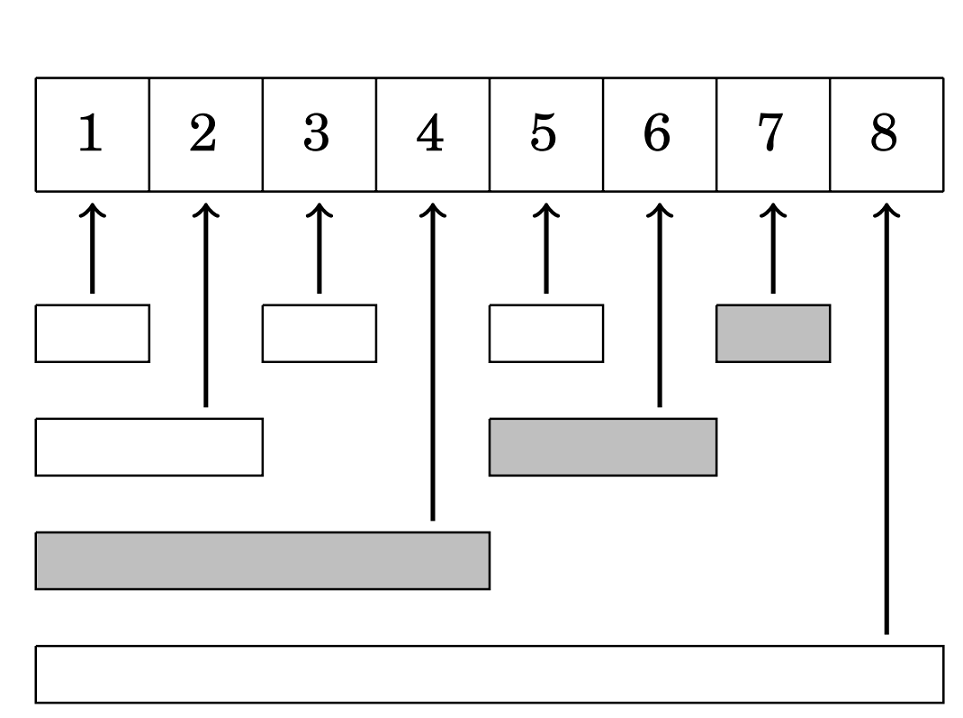
Programski kod za računanje sume prefiksa koristeći Fenwickovo stablo:
// suma intervala [1, index]
int prefixSum(int index, vector <int> &fenwickTree) {
int sum = 0;
while(index >= 1) {
sum += fenwickTree[index];
index -= index & -index;
}
return sum;
}
Promjena vrijednosti elementa niza
Dodavanje nekog broja elementu originalnog niza se vrši na sličan način kao i računanje sume prefiksa, samo ovaj put se kreće od manjeg indeksa prema većima. Kao primjer ćemo uzeti broj na indeksu 3, a cilj nam je promijeniti vrijednost za svim elementima Fenwickovog stabla koji prestavljaju sumu u kojoj se nalazi element na indeksu 3. Idemo obrnutim smjerom nego prije.
Prvo ažuriramo Fenwickovo stablo na indeksu 3:
Zatim indeksu dodajemo posljednji postavljeni bit (1) i dobijemo 4.
Mijenjamo vrijednost Fenwickovog stabla na indeksu 4:
Novi index: 8
...
postupak se nastavlja dok indeks ne prijeđe granice niza.
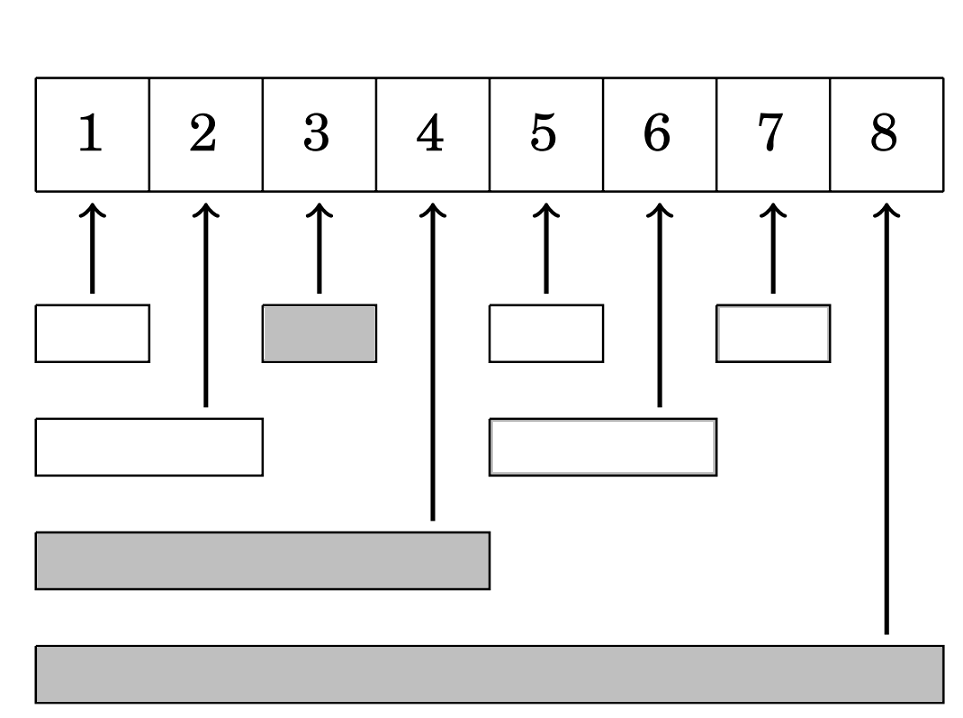
Programski kod je vrlo sličan onomu za dohvaćanje sume prefiksa:
//elementu na poziciji index dodaje x
void update(int index, int x, vector <int> &fenwickTree) {
while(index < fenwickTree.size()) {
fenwickTree[index] += x;
index += index & -index;
}
}
U ovoj implementaciji ne označava pravu veličinu niza.
Ona je zapravo za 1 manja zbog nultog indeksa kojeg tu ne koristimo.
Koristeći ovu funkciju možemo iz bilo kojeg niza izgraditi Fenwickovo stablo:
/*
vraća Fenwickovo stablo za dani niz arr.
pretpostavimo da se radi o 1-indeksiranju
*/
vector <int> getFenwick(vector <int> arr) {
vector <int> fenwickTree(arr.size(), 0);
for(int i = 1; i < arr.size(); ++i) {
update(i, arr[i], fenwickTree);
}
return fenwickTree;
}
Sada efikasno možemo odgovoriti na upite o sumi nekog podniza od do na isti način kao kod niza suma prefiksa:
Korištenje 1-indeksiranja nam pokriva rubni slučaj kad se pozove za indeks 0.
Ovime smo pokrili promjene nad jednim elementom i upite nad intervalima. Pogledajmo sada kako obavljati promjene nad intervalima i upite nad jednim elementom.
Range update, point query
Kako bi ovo postigli, potrebno je podsjetiti se difference arraya.
Kako bi intervalu promijenili vrijednost za , potrebno je elementu na indeksu dodati , a onom na indeksu oduzeti.
Dohvaćanje vrijednosti je također isto kao kod niza razlika, potrebno je napraviti sumu prefiksa. Prednost je u tome što se dohvaćanje elementa koristeći Fenwickovo stablo obavlja u .
Programski kodovi
void rangeUpdate(int l, int r, int x, vector <int> &fenwickTree) {
update(l, x, fenwickTree);
update(r + 1, -x, fenwickTree);
/*
nije potrebno provjeravati je li r + 1 izvan granica
jer while(index < fenwickTree.size()) rješava taj slucaj
*/
}
// vraca vrijednost elementa na indeksu i
void pointQuery(int i, vector <int> &fenwickTree) {
return prefixSum(i, fenwickTree);
}