Sparse table

Autor: Adrian Brajković

Uvod

Sparse table je struktura podataka koja nad statičkim nizovima može obaviti min/max upite nad intervalima u $O(1)$. Kako bismo to ostvarili, potrebno je nad nizom obaviti pretprocesiranje i izgraditi sparse table. Složenost pretprocesiranja je $O(n*log(n))$. Ovdje ćemo prikazati funkcionalnosti koristeći sparse table za min upite, a analogno se gradi i za max upite. Cilj nam je imati zapisano u matrici rješenja min upita za sve duljine koje su potencije broja 2. Dakle, imamo matricu $sparseTable[i][j]$, gdje $i$ predstavlja indeks početka intervala, a $j$ predstavlja eksponent pri potenciranju broja 2 što označava duljinu intervala.

Primjer:
$sparseTable[3][0]$ - minimalni broj na intervalu koji počinje na indexu 3, a duljine je $2^{\smash{0}} = 1$
$sparseTable[2][1]$ - početak intervala je 2, a on je duljine $2^{\smash{1}} = 2$
$sparseTable[1][2]$ - početak intervala je 1, a on je duljine $2^{\smash{2}} = 4$

Ako ovo prikažemo formulom:

$$sparseTable[i][j] = min(array[i], array[i + 1], ..., array[i + 2^{\smash{j}} - 1])$$

Pretprocesiranje

Prvi korak je upisati rješenja za sve duljine 1 (kad je $j = 0$). U tom slučaju samo prepišemo vrijednosti iz početnog niza:

$$sparseTable[i][0] = array[i];$$

Imamo rješenja za intervale: $[0, 0], [1, 1], [2, 2], ...$

Sad računamo za intervale duljine 2 $([0, 1], [1, 2], [2, 3], ...)$.
Primijetimo da se svaki taj interval može izračunati pomoću intervala duljine 1 koje već imamo zapisane.
Minimalni broj na intervalu $[0, 1]$ je manji od $min[0, 0]$ i $min[1, 1]$.
Nadalje, $min[1, 2] = min(min[1, 1], min[2, 2])$, i tako za svaki element niza (osim zadnjeg, jer iz njega ne može početi interval duljine 2).

Kako to prikazati pomoću naše matrice?

$$sparseTable[0][1] = min(sparseTable[0][0], sparseTable[1][0])$$ $$sparseTable[1][1] = min(sparseTable[1][0], sparseTable[2][0])$$ $$sparseTable[2][1] = min(sparseTable[2][0], sparseTable[3][0])$$ $$sparseTable[3][1] = min(sparseTable[3][0], sparseTable[4][0])$$ $$...$$

Nastavljamo s intervalima duljine 4 $(j = 2)$. Primijetimo da se interval $[0, 3]$ može prikazati kao unija intervala $[0, 1]$ i $[2, 3]$, a podatak o najmanjem broju za ta dva intervala smo već izračunali.
Vrijedi:

$$sparseTable[0][2] = min(sparseTable[0][1], sparseTable[2][1])$$ $$sparseTable[1][2] = min(sparseTable[1][1], sparseTable[3][2])$$ $$...$$

Postupak se nastavlja za sve $j$ dok je duljina intervala $2^{\smash{j}}$ manja ili jednaka duljini niza.

Primjer pretprocesiranja

Pogledajmo sljedeći primjer:
Imamo niz duljine $N = 8$, $[1, 3, 5, 8, 6, 1, 4, 2]$ i iz njega je potrebno napraviti sparse table. Ispod se nalazi slika kako bi lakše vizualizirali postupak.

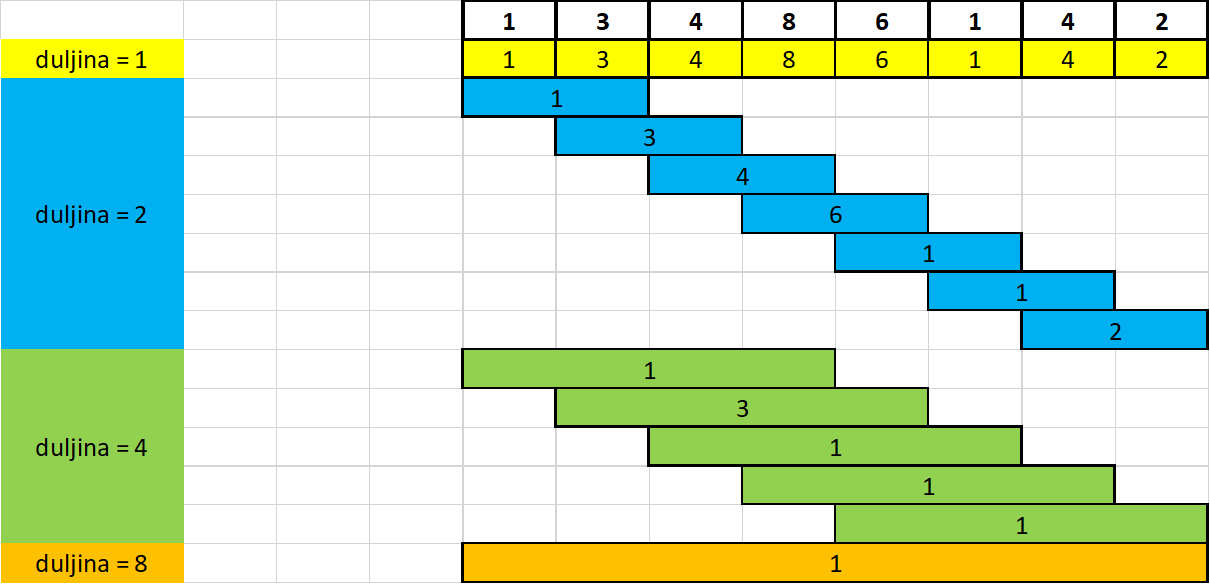
Prvo ispunjavamo sparseTable za $j = 0$ $(duljina\_intervala = 2^{\smash{0}} = 1)$ - žuti redak sa slike. Kao što je prije rečeno, samo prepišemo vrijednosti iz niza.

Nakon toga, za $j = 1$ $(duljina\_intervala = 2^{\smash{1}} = 2)$ - plavi dio sa slike, računamo $sparseTable[i][1]$ gdje vrijedi $0 \le i \lt N - 1$ koristeći podatke iz prošlog koraka. Npr. za $sparseTable[3][1]$ (interval $[3, 4]$) uzet ćemo $sparseTable[3][0] = 8$ (interval $[3, 3]$) i $sparseTable[4][0] = 6$ (interval $[4, 4]$), a manji od ta dva broja zapisujemo kao rezultat.

Nastavljamo s $j = 2 (duljina\_intervala = 2^{\smash{2}} = 4)$. Opet računamo rješenje koristeći rezultate iz prošlog koraka. Na sljedećim slikama je prikazano koja polja se koriste prilikom računanja rezultata.

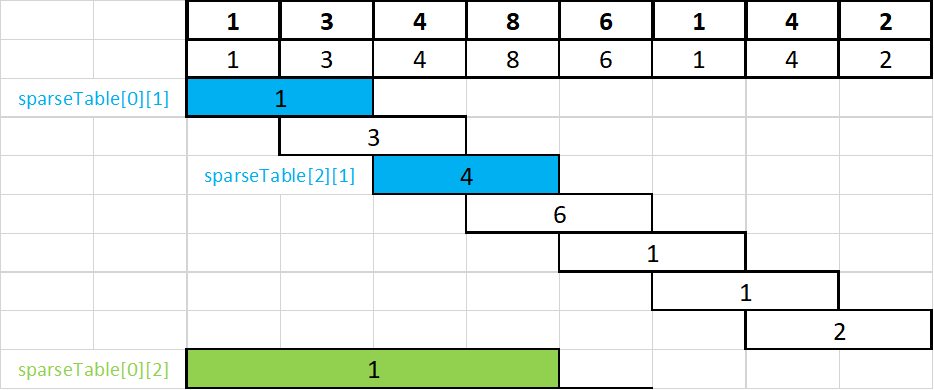
$$sparseTable[0][2] = min(sparseTable[0][1], sparseTable[2][1])$$

 
 

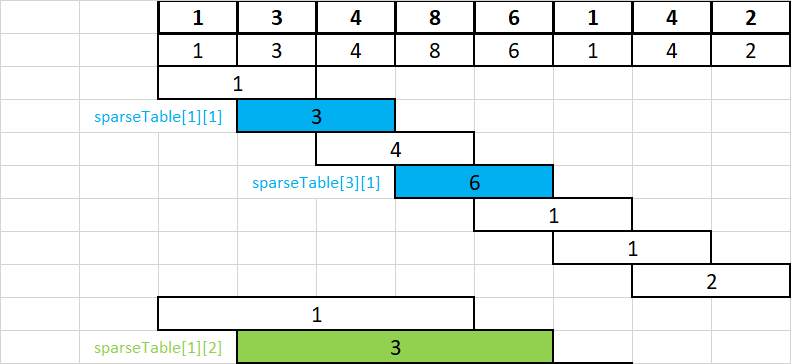
$$sparseTable[1][2] = min(sparseTable[1][1], sparseTable[3][1])$$

Postupak se nastavlja dok je $i + 2^{\smash{j}} - 1 < N$, tj. dok interval ne izlazi iz granica niza.

 
 

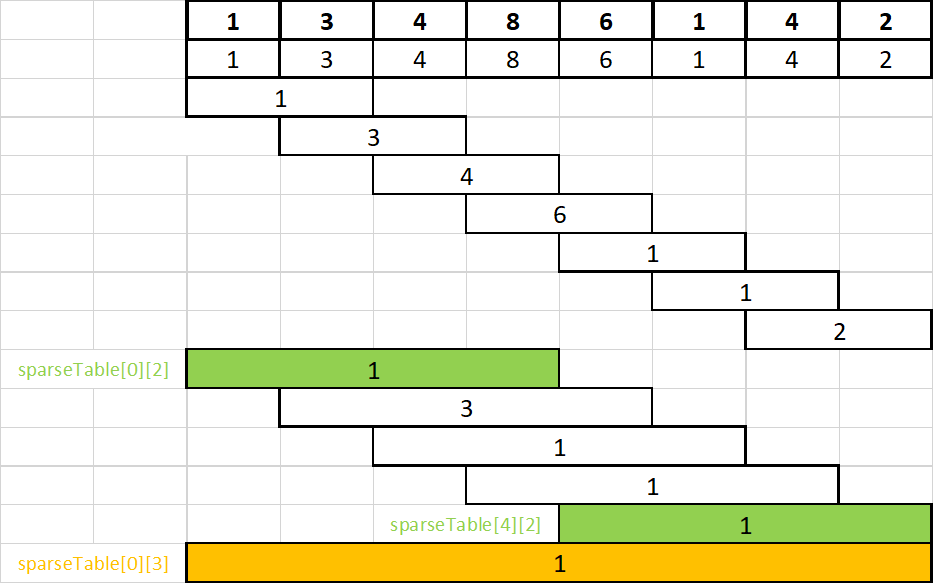
$$sparseTable[0][3] = min(sparseTable[0][2], sparseTable[4][2])$$

Ovime smo završili pretprocesiranje i izgradili sparse table.
Formula:

$$sparseTable[i][j] = min(sparseTable[i][j-1], sparseTable[i + 2^{\smash{j-1}}][j-1])$$

Zašto baš $i + 2^{\smash{j-1}}$? Jer nam treba desna polovica intervala duljine $2^{\smash{j}}$, dakle početnom indeksu pridodajemo pola duljine niza.

Programski kod

vector < vector<int> > createSparseTable(vector <int> arr) {
	int N = arr.size();
	int K = log2(N); //2^K je najveca duljina intervala koja ne prelazi duljinu niza

	vector <int> row(K + 1);
	vector < vector<int> > sparseTable(N, row);

	for(int i = 0; i < N; i++) { // j = 0
		sparseTable[i][0] = arr[i]; 	  //intervali duljine 2^0 = 1
	}

	for(int j = 1; j <= K; ++j) {
		int len = pow(2, j); //duljina intervala

		for(int i = 0; i + len - 1 < N; ++i) { //uvjet je da interval [i, i + 2^j - 1] ne prelazi izvan granica niza
			sparseTable[i][j] = min(sparseTable[i][j - 1], sparseTable[i + len/2][j - 1]);
		}
	}


	return sparseTable;
}

Napomena

Često se umjesto $pow(2, n)$ koristi logički posmak ulijevo (engl. bitshift) za potencije broja 2. $(1 << n)$

Upiti

Kako sada odgovoriti na upit za najmanji broj nad nekim intervalom? Uzmemo najveću potenciju broja 2, a da ne prelazi duljinu intervala. Na primjer, tražimo rješenje za interval $[2, 7]$. Najveća potencija broja 2 u ovom slučaju je 4.
Vrijedi $j = 2$ i sad radimo upit za $sparseTable[2][j]$ (početak intervala je 2, a duljina $2^{\smash{j}} = 4$). Osim toga uzimamo upit i za desni dio intervala, točnije $[4, 7]$, a to je $sparseTable[7 - 2^{\smash{j}} + 1][j]$. Uzmemo manju vrijednost i ona je rješenje.
Možemo vidjeti da ta dva upita uistinu pokrivaju cijeli interval.

Konačno, formula za dohvat najmanjeg broja na intervalu $[L, R]$ (duljina intervala = R - L + 1):

$$min(sparseTable[L][j], sparseTable[R - 2^{\smash{j}} + 1][j])$$ $$j = floor(log2(R - L + 1))$$