Zapisi grafova

Autor: Ivan Vlahov

Grafovi se u memoriji mogu prikazati na više načina, a različiti algoritmi često koriste i različite načine prikazivanja u memoriji kako bi na efikasan način riješili određeni problem. U ovom poglavlju proći ćemo kroz najčešće metode zapisa grafova.

Lista susjedstva

Lista susjedstva (eng. adjacency list) je metoda zapisa grafova u kojoj za svaki čvor pamtimo sve njegove susjede. U C++-u se ovaj zapis može realizirati korištenjem vektora vektora:

// n je broj vrhova

int n = 3;

// vrhovi se numeriraju od 0 do n-1
// stvaramo vector s n vectora cijelih brojeva

vector<vector<int>> adjList(n);

// adjList[i] predstavlja listu susjeda vrha i

adjList[0] = {1, 2};
adjList[1] = {0};
adjList[2] = {0};

Lista susjedstva iz gornjeg primjera predstavlja graf na slici:

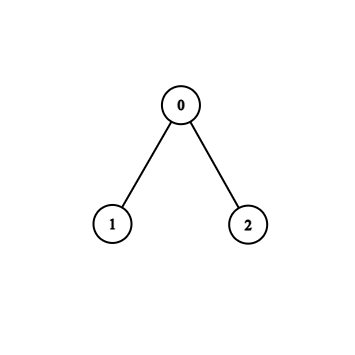
U slučaju da se radi o težinskom grafu, listu susjedstva ćemo zapisati kao vektor vektora parova vrh-težina. Ako se radi o usmjerenom grafu, onda vrh $j$ dodajemo u listu susjedstva vrha $i$ samo ako postoji brid od vrha $i$ do vrha $j$.

// DW kao Directed i Weighted
vector<vector<pair<int, int>>> adjListDW(n);

adjListDW[0] = {{2, 2}};
adjListDW[1] = {{0, 3}};

Lista susjedstva iz gornjeg primjera predstavlja graf na slici:

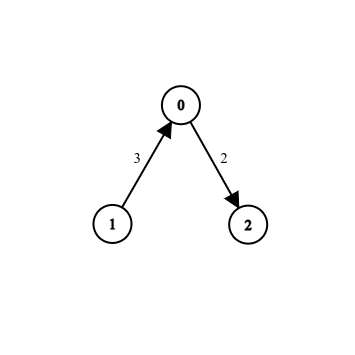
Matrica susjedstva

Drugi način zapisa grafova u memoriji jest korištenjem matrice susjedstva (eng. adjacency matrix). Ako se graf sastoji od $n$ vrhova, matrica susjedstva je matrica $G$ dimenzija $n \times n$ za koju vrijedi sljedeće:

$$G_{i,j} = \left\{ \begin{array}{l} w_{i,j}, \text{ ako postoji brid od i do j}\\ 0, \text{ inače} \end{array} \right.$$

U slučaju da graf nije težinski, matrica susjedstva može biti i jednostavnije zapisana:

$$G_{i,j} = \left\{ \begin{array}{l} 1, \text{ ako postoji brid od i do j}\\ 0, \text{ inače} \end{array} \right.$$

Ako graf nije usmjeren, matrica susjedstva je simetrična jer za svaki brid $(i, j)$ vrijedi $w_{i,j} = w_{j, i}$.

U memoriji matricu susjedstva zapisujemo kao dvodimenzionalno polje:

int adjMatrix[3][3] = {
  {0, 0, 2},
  {3, 0, 0},
  {0, 0, 0}
};

Ovaj primjer predstavlja isti graf kao i drugi primjer iz liste susjedstva.

Lista bridova

Sljedeći način zapisa je lista bridova (eng. edge list). Lista bridova je lista parova vrhova između kojih postoji brid te se u C++-u može implementirati kao vektor parova cijelih brojeva za netežinske grafove, ili kao vektor trojki (dva vrha i težina) za težinske grafove. Razlike u implementaciji između usmjerenih i neusmjerenih grafova nema, samo u slučaju usmjerenih grafova moramo odrediti na koje ćemo mjesto u paru vrhova upisivati vrh u kojem brid započinje, a na koje ćemo upisat vrh u kojem brid završava. Intuitivno se čini najboljim na prvo mjesto staviti početni, a na drugo završni vrh.

// Primjer s prve slike 
// Netezinski neusmjereni graf

vector<pair<int, int>> edgeList;
edgeList.push_back({0, 1});
edgeList.push_back({0, 2});

// Primjer s druge slike
// Tezinski usmjereni graf

vector<tuple<int, int, int>> edgeListDW;
edgeListDW.push_back({1, 0, 3});
edgeListDW.push_back({0, 2, 2});

Prilikom rada s tupleovima, trebat ćete pristupati pojedinim komponentama. Jednostavan način za pristup je korištenjem funkcija get<> i tie:

for(auto &edge : edgeListDW) {

  // get<> pristupa pojedinim elementima tuplea,
  // u ovom slučaju element na indeksu 2 (težini brida)

  cout << get<2>(edge) << " ";

  // tie je nešto kao unpacking operator u Pythonu,
  // ili kao destructuring u Javascriptu,
  // sprema pojedine elemente tuplea u zadane varijable

  int a, b, w;
  tie(a, b, w) = edge;

  // ispisuje vrhove brida

  cout << a << " " << b << "\n";

}

Ispis gornjeg isječka koda:

3 1 0
2 0 2

Više informacija o tie i get.

savjet

Osim tuplea, za listu bridova možete koristiti i pair<pair<int, int>, int>. Također, poredak unutar vanjskog para može biti koristan, npr. ako koristimo pair<int, pair<int, int>>, sortiranjem vektora ovakvih parova dobit ćemo vektor sortiran po težinama od najmanje do najveće, što je u nekim algoritmima dosta korisno, kao npr. u Kruskalovom algoritmu koji ćemo obraditi u članku o pronalasku najmanjeg razapinjućeg stabla.

Polje roditelja

Ako radimo s ukorijenjenim netežinskim stablima, za prikaz grafa dovoljno nam je za svaki vrh znati njegovog roditelja. Pošto korijen nema roditelja, za njegovog roditelja možemo upisati njega samog ili $-1$.

int parents[4] = {-1, 0, 0, 1};

Gornji primjer prikazuje sljedeći graf, u kojem je korijen vrh $0$:

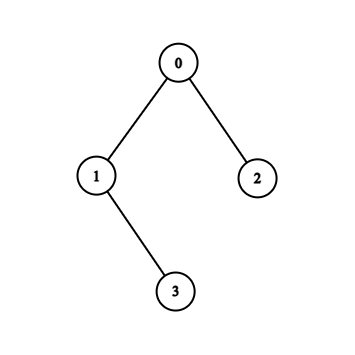
Implicitni zapis

U nekim problemima, kada graf ima jako puno čvorova i jako puno bridova, nemoguće je spremiti sve bridove u neku od gore navedenih struktura, ali i dalje moramo za zadani vrh moći odrediti njegove susjede. U tom slučaju graf se često zadaje implicitno - za svaki vrh postoji nekakva metoda kojom možemo odrediti bridove kojima je taj vrh povezan s drugim vrhovima.

Ne postoji neki jedinstveni implicitni zapis - on ovisi od problema do problema, pa je zato i najbolje ovakav zapis objasniti na primjeru.

Recimo da graf ima $2^{30}$ vrhova numeriranih od $0$ do $2^{30} - 1$, te da je zadano da su dva vrha povezana bridom ako i samo ako se njihovi indeksi u binarnom zapisu razlikuju u jednom bitu. Jednostavno možemo zaključiti da svaki vrh ima 30 susjeda, što znači da ovaj graf ima $(30 * 2^{30}) / 2 = 16106127360$ bridova, što je previše bridova za upisati u memoriju. Iako ne možemo zapisati bridove u memoriju, i dalje ih, zbog toga što je graf zadan implicitno, možemo jako jednostavno odrediti za svaki od vrhova.

// izvan maina

void findNeighbours(int node, vector<int> &neighbours) {
  for(int i=0; i<30; i++) {
    // flippamo i-ti bit
    neighbours.push_back(node ^ (1 << i));
  }
}

// main

// recimo da nas zanima vrh 1620
int node = 1620;

// vektor u koji cemo spremiti susjede vrha 
vector<int> neighbours;
findNeighbours(node, neighbours);

// recimo da je binary() neka nasa funkcija koja vraca
// 30-bitnu binarnu reprezentaciju broja kao string

cout << "Node:\n" << binary(node) << "\n\n";

cout << "Neighbours:\n";
for(auto &ngb : neighbours) {
  cout << binary(ngb) << "\n";
}

Ispis:

Node:
000000000000000000011001010100

Neighbours:
000000000000000000011001010101
000000000000000000011001010110
000000000000000000011001010000
000000000000000000011001011100
000000000000000000011001000100
000000000000000000011001110100
000000000000000000011000010100
000000000000000000011011010100
000000000000000000011101010100
000000000000000000010001010100
000000000000000000001001010100
000000000000000000111001010100
000000000000000001011001010100
000000000000000010011001010100
000000000000000100011001010100
000000000000001000011001010100
000000000000010000011001010100
000000000000100000011001010100
000000000001000000011001010100
000000000010000000011001010100
000000000100000000011001010100
000000001000000000011001010100
000000010000000000011001010100
000000100000000000011001010100
000001000000000000011001010100
000010000000000000011001010100
000100000000000000011001010100
001000000000000000011001010100
010000000000000000011001010100
100000000000000000011001010100